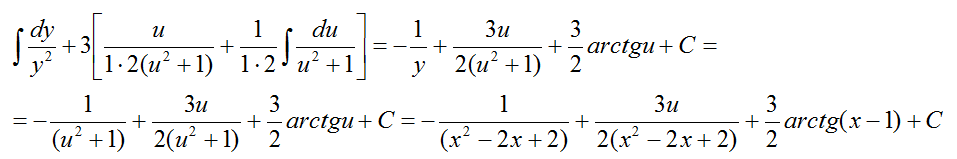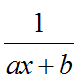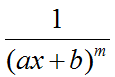Простыми или элементарными называются дроби, следующих типов (всего их 4 типа):

---

1. 
   

   ---

2. 
   

   ---

3. 
   

   ---

4. 
   

   ---

где m, n – натуральные числа и m≥2, n≥2, D=b² – 4ac<0.

---

Интегрирование простых дробей 1-ого и 2-ого типов.

Формула для интегрирования дробей первого типа: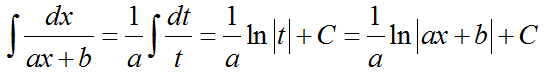
Формула для интегрирования дробей второго типа: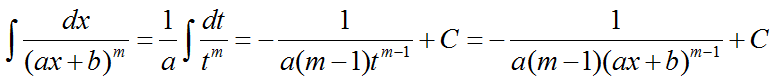
Решения первого и второго типов интегралов просты. Преобразуются к табличному виду за счёт подстановки t = ax + b.
Рассмотрим примеры решений интегралов простых дробей первого и второго типов.

---

1.

---

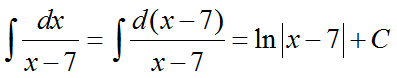
2.

---

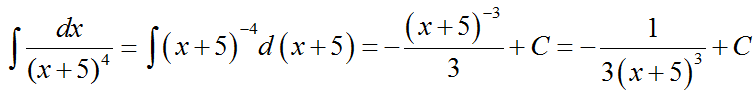
3.

---

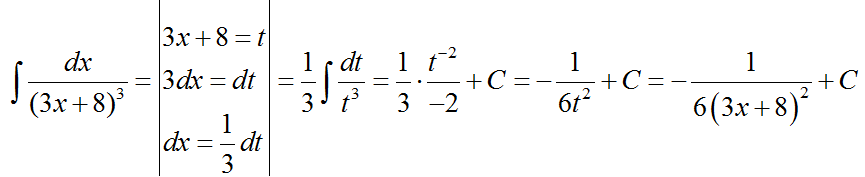
4.  

---

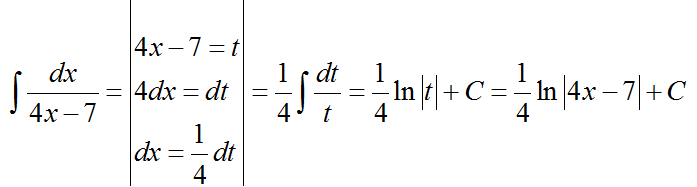
Интегрирование простых дробей 3-ого типа.

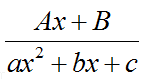
Общее решение уравнения третьего типа можно представить формулой:

Рассмотрим пример интегрирование простой дроби третьего типа

---

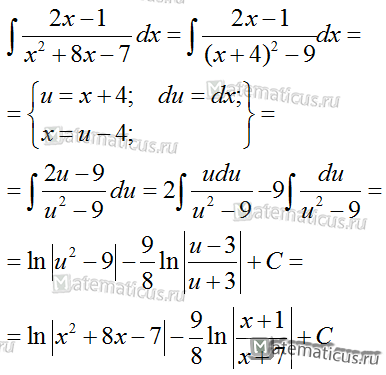
Интегрирование простых дробей 4-ого типа.

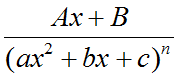
Общее решение такого уравнения можно представить формулой:

Здесь первый интеграл находим с помощью подстановки — t = u² +s и преобразовываем к табличному виду $\int {\frac{{dt}}{{{t^n}}}} $, второй — используя рекуррентную формулу и метод интегрирования по частям:

---

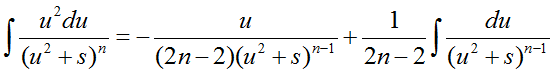
Рассмотрим пример интегрирование простой дроби четвертого типа:
Пример
  
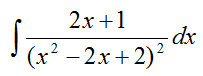
Решение

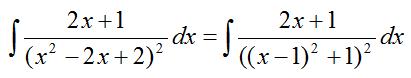
Пусть u=x-1, тогда x=u-1 и du=dx, получаем

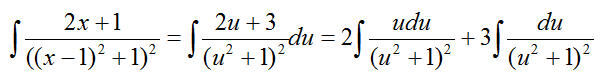
Сделаем подстановку для правого выражения.
Пусть y=u²+1, тогда dy=2udu и воспользуемся формулой

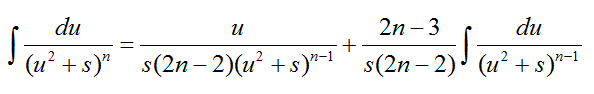
имеем