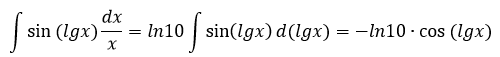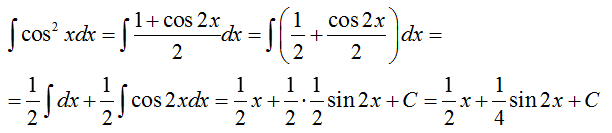Интегрирование тригонометрических функций

Для нахождения интегралов от тригонометрических функций вида:

∫cos²ⁿx dx

∫sin²ⁿx dx

где n – целое положительное число.

применяют тригонометрические формулы понижения степени:

${\sin ^2}\alpha = \frac{{1 — \cos 2\alpha }}{2}$

${\cos ^2}\alpha = \frac{{1 + \cos 2\alpha }}{2}$

$\sin x \cdot \cos x = \frac{1}{2}\sin 2x$

---

Пример 1

Найти интеграл от функции

∫cos²x dx

Решение

---

Пример 2

Найти интеграл от функции

∫sin⁴x dx

Решение

---

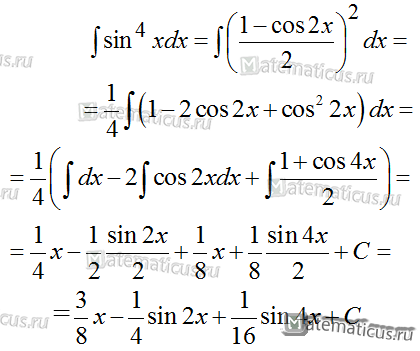
Вычисление интеграла вида:

∫sin²ⁿ⁺¹x dx

∫cos²ⁿ⁺¹x dx

Для первой функции применяем функцию cosx, для второй — sinx.

---

Пример 3

Найти интеграл от функции

∫cos³x dx

Решение

∫cos³x dx = ∫cos²x cosx dx = 

= ∫(1-sin²x) cosx dx =

= ∫cosx dx + ∫sin²x cosx dx =

= sinx — 1/3sin³x + C

---

Для вычисления интегралов от тригонометрических функций вида:

∫cos^mx dx

∫sinⁿx dx

где одно из чисел m или n – нечетное.

Вводят вспомогательную тригонометрическую функцию, sinx (если n — нечетно), cosx (если m — нечетно).

Также если функция четная относительно sinx и cosx, можно воспользоваться подстановкой u=tgx.

---

Пример 4

Найти интеграл от функции

∫cos⁴x sin³x dx

Решение

Подынтегральное выражение представим в виде:

cos⁴x sin²x d(-cosx) = -cos⁴x (1-cos²x) d(cosx)

получаем

---

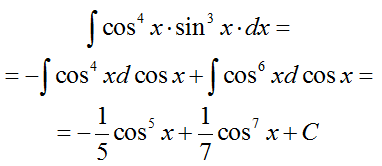
Пример 5

Найти интеграл от функции

∫sin³6xсos6x dx

Решение

---

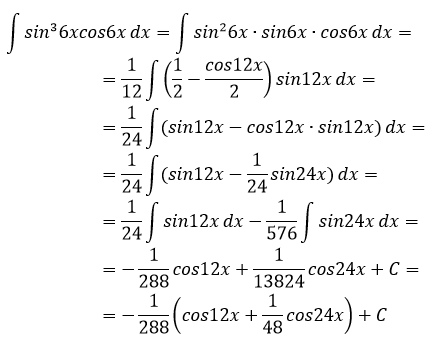
Для вычисления интегралов вида:

∫sin mx cos nx dx 

∫cos mx cos nx dx 

∫sin mx sin nx dx 

удобно применять тригонометрические формулы произведения:

∫sin mx cos nx dx = 1/2 [sin(m-n)x + sin(m+n)x]

∫cos mx cos nx dx = 1/2 [cos(m-n)x — cos(m+n)x]

∫sin mx sin nx dx = 1/2 [cos(m-n)x + cos(m+n)x]

---

Пример 6

Найти интеграл

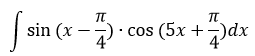
Решение

---

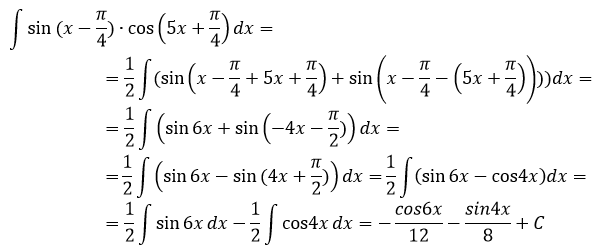
Пример 7

Вычислить интеграл от функции

∫sin2x sin5x dx

Решение

---

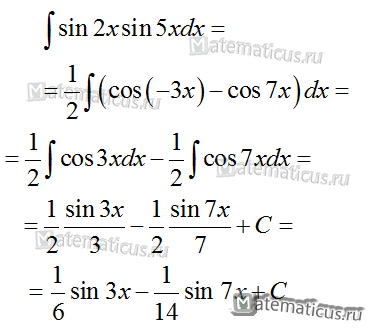
Для вычисления интегралов от тригонометрических функций вида:

∫tg^mx dx

∫ctgⁿx dx

применяют множитель tg²x или ctg²x которые преобразовываются в равенства:

$$\eqalign{& 1 + t{g^2}x = \frac{1}{{{{\cos }^2}x}}  \cr & 1 + ct{g^2}x = \frac{1}{{{{\sin }^2}x}} \cr} $$

---

Пример 7

Найти интеграл от функции

∫tg³x dx

Решение

---

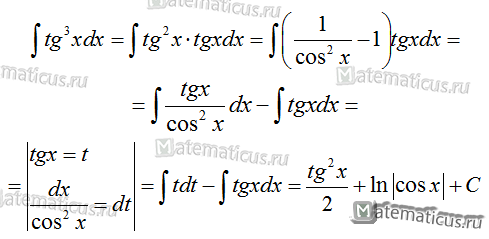
Пример интегрирования с другими тригонометрическими функциями.

Пример 8

Найти интеграл

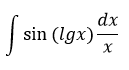
Решение