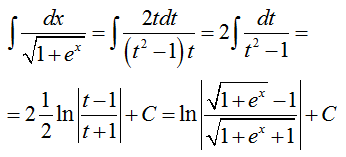Если функция f(x) имеет первообразную и при этом x=φ(t) дифференцируема и непрерывна, тогда для интегрирования функции можно воспользоваться формулой:
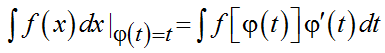
Рассмотрим примеры.
Пример
$$\int {\frac{{dx}}{{\sqrt {1 + {e^x}} }}} dx$$
Решение
Чтобы избавиться от корня, сделаем подстановку, пусть $1 + {e^x} = {t^2}$, тогда имеем $t = \sqrt {1 + {e^x}} $.
Для того чтобы найти dx, продифференцируем выражение $1 + {e^x} = {t^2}$, получим
$$d\left( {1 + {e^x}} \right) = d\left( {{t^2}} \right)$$
$${e^x}dx = 2tdt$$
$$dx = \frac{{2tdt}}{{{e^x}}} = \frac{{2tdt}}{{{t^2} — 1}}$$
В итоги получим интеграл:
$$\int {\frac{{du}}{{{u^2} — {a^2}}}} $$