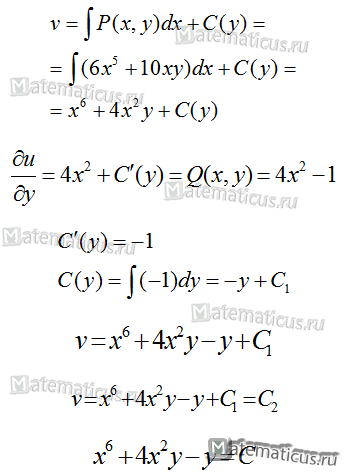Уравнение вида:
P(x,y)dx + Q(x,y)dy = 0
называется уравнением в полных дифференциалах.
При этом функции P(x,y) и Q(x,y) должны удовлетворять равенству:
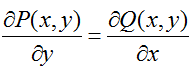
Пусть левая часть уравнения
P(x,y)dx + Q(x,y)dy = 0
представляет собой полный дифференциал некоторой функции F(x,y), тогда найти эту функцию можно через уравнение:
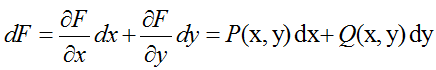
Тогда общем решением уравнения будет:
F(x,y) = 0
Пример
Решить уравнение
$$(6{x^5} + 8xy)dx + (4{x^2} — 1)dy = 0$$
Решение
Проверим условие:
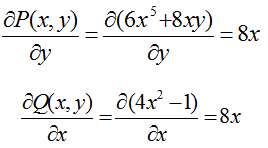
Условие выполнено, значит данное дифференциальное уравнение относится к уравнению в полных дифференциалах.
Найдём функцию v.