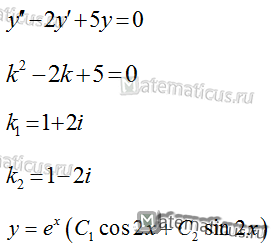Если дифференциальное уравнение имеет вид:
y′′ + py’ + qy = 0
то такое уравнение называется линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами
p, q — числа или постоянные коэффициенты
Для решения искомого уравнения необходимо записать характеристическое уравнение вида
k2 + pk + q = 0
Корни характеристического уравнения можно найти через дискриминант
D = p2 – 4q
В характеристическом уравнении три случая различных корней, перечислим их:
- Если D>0, то уравнение имеет два действительных и различных корня:
$${k_{1,2}} = \frac{{ — p \pm \sqrt {{p^2} — 4q} }}{2}$$
k1 ≠ k2
k1, k2 – корни уравнения
тогда запишем общее решение уравнения:
![]()
II. Если D=0, то уравнение имеет один действительный корень:
$${k_{1,2}} = \frac{{ — p}}{2}$$
k1 = k2 = k
k – корень уравнения
отсюда получим общее решение уравнения:
![]()
III.
Если D<0, то уравнение имеет пару комплексных корней:
$${k_{1,2}} = \frac{{ — p \pm i\sqrt D }}{2}$$
k1,2 = α±iβ
k1, k2 – корни уравнения
α — действительная часть корня
β — мнимая часть корня
запишем общее решение уравнения:
![]()
Пример 1
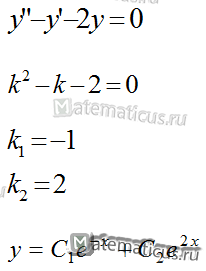
Пример 2
Найдите общее решение дифференциального уравнения второго порядка с постоянными коэффициентами:
$$y′′ -6y’ + 9y = 0$$
$${k^2} — 6k + 9 = 0$$
$${k_{1,2}} = 3$$
$$y = {e^{ 3x}}({C_1} + x{C_2})$$
Пример 3