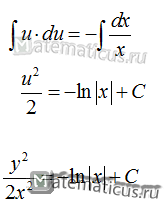Дифференциальное однородное уравнение первого порядка

Решение дифференциального однородного уравнения первого порядка

Если дифференциальное уравнение имеет вид:

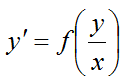
решается заменой неизвестной функции выражением:

$$u = \frac{y}{x}$$

$$y = u \cdot x$$

$$y’ = u’x + u$$

функцию u можно найти через уравнения с разделяющими переменными

$$u’x + u = f(u)$$

$$\frac{{du}}{{dx}}x = f(u) — u$$

---

Пример 1

Решить дифференциальное уравнение

$$y’ = ctg\frac{y}{x} + \frac{y}{x}$$

Решение

Сделаем замену неизвестной функции

$$u = \frac{y}{x}$$

$$y = ux$$

$$y’ = u’x + u$$

$$u’x + u = ctgu + u$$

$$\frac{{du}}{{dx}}x = ctgu$$

Отсюда получим дифференциальное уравнение с разделяющими переменными

$$\frac{{du}}{{ctgu}} = \frac{{dx}}{x}$$

проинтегрируем оба выражения, получим

$$\int {\frac{{\sin u}}{{\cos u}}} du = \int {\frac{{dx}}{x}} $$

$$\ln |\operatorname{cosu} | = \ln |x| + lnC$$

$$\operatorname{cosu}  = Cx$$

$$\cos \frac{y}{x} = Cx$$

$$\frac{y}{x} = \arcsin (Cx)$$

Отсюда получаем y

$$y = x\arcsin (Cx)$$

---

Пример 2

Решите дифференциальное уравнение:

(x² — y²)dx — xydy = 0

Решение

Выполним преобразования уравнения

(x² — y²)dx — xydy = 0

и приведём к виду

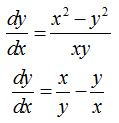
Сделаем подстановку вида

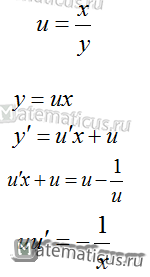
получаем решение уравнения