Численное решение дифференциального уравнения методом Рунге-Кутты

Основная идея метода Рунге-Кутты заключается в приближенном вычислении следующего значения функции, используя информацию о скорости изменения функции в нескольких точках между текущим моментом времени и следующим. Метод Рунге-Кутты обеспечивает баланс между точностью и вычислительной сложностью.

Метод Рунге-Кутты четвёртого порядка для численного решения дифференциальных уравнений (ОДУ) вычисляется по формулам:

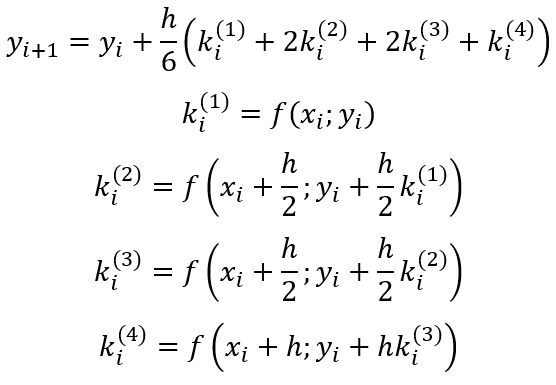
Метод Рунге-Кутты второго порядка формулы:

---

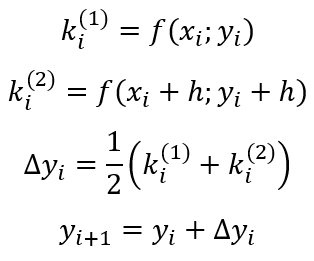
Пример

Решите обыкновенноеи дифференциальное уравнение численным методом Рунге-Кутты второго порядка

y’=3x²y

y(0)=1

шаг h=0,05 на отрезке [0;1]
Решение

Решиние обыкновенного дифференциального уравнения методом Рунге-Кутты второго порядка приведено в таблице

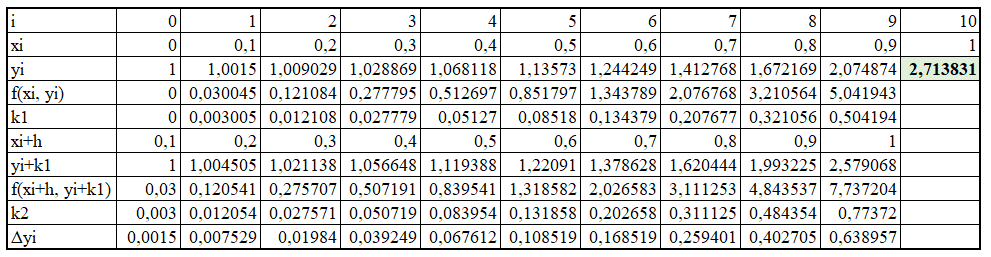
Решение дифференциальное уравнение точным методом:

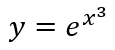
Метод Рунге-Кутты громоздкий, особенно VI порядка, но точность выше, чем у метода Эйлера.