Уравнение плоскости, проходящей через три точки

Если плоскость проходит через три точки М₁(x₁;y₁;z₁), M₂(x₂;y₂;z₂) и M₃₍x₃;y₃;z₃), не лежащие на одной прямой, то проходящая через них плоскость представляется уравнением плоскости проходящей через 3 точки:

 

 

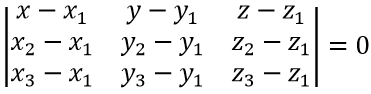
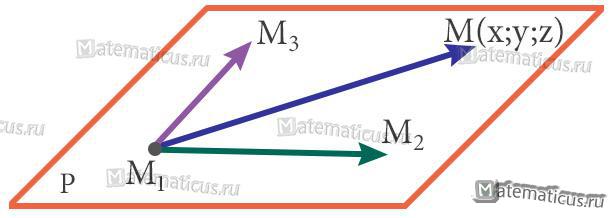
При этом, векторы $\overrightarrow {{M_1}{M_2}} $={X₂-X₁;Y₂-Y₁;Z₂-Z₁} и $\overrightarrow {{M_1}{M_3}} $={X₃-X₁;Y₃-Y₁;Z₃-Z₁} не коллинеарны.

Точка М(х; у; z) лежит в одной плоскости с точками M₁, M₂ и M₃ только в том случае, когда векторы:

$\overrightarrow {{M_1}{M_2}} $,  $\overrightarrow {{M_1}{M_3}}$ и $\overrightarrow {{M_1}{M}}$={X-X₁;Y-Y₁;Z-Z₁} компланарны.

---

Пример

Точки M₁(2;3;1), M₂(1;2;2) и M₃(1;5;4)  не лежат на одной прямой, так как

векторы  $\overrightarrow {{M_1}{M_2}} $={1-2; 2-3; 2-1}={-1; -1; 1} и $\overrightarrow {{M_1}{M_3}} $={1-2; 5-3; 4-1}={-1; 2; 3} не коллинеарны (не параллельны).

Плоскость с точками M₁, M₂ и M₃ представляется уравнением

$\left| {\begin{array}{*{20}{c}}{x — 2}&{y — 3}&{z — 1} \\ { — 1}&{ — 1}&1 \\ { — 1}&2&3 \end{array}} \right| = 0$

$\left( {x — 2} \right)\left| {\begin{array}{*{20}{c}} { — 1}&1 \\ 2&3 \end{array}} \right| — \left( {y — 3} \right)\left| {\begin{array}{*{20}{c}}{ — 1}&1 \\ { — 1}&3 \end{array}} \right| + \left( {z — 1} \right)\left|{\begin{array}{*{20}{c}}{ — 1}&{ — 1} \\ { — 1}&2 \end{array}} \right| = 0$

 

$ \left( {x — 2} \right)\left( { — 1\cdot3 — 2\cdot1} \right) — \left( {y — 3} \right)\left( { — 1\cdot3 — 1\cdot — 1} \right) + \left( {z — 1} \right)\left( { — 1\cdot2 — \left( { — 1} \right)\cdot — 1} \right) = 0$

Получаем уравнение

5x-2y+3z-7=0