Уравнение плоскости в отрезках на осях

Расстояние от точки до плоскости, как найти, пример, решение, формула, в пространстве, от точки до плоскости, расстояние, длина
Если плоскость Ax + By + Cz + D = 0 отсекает на осях отрезки (не равные нулю) а, b, с, то ее можно представить в виде уравнения:

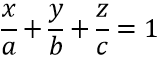
Это уравнение и есть уравнение плоскости в отрезках

а, b, с — отрезки, отсекаемые плоскостью на координатных осях и находятся по формулам:

отрезок на осях OX:

$a =  — \frac{D}{A}$, A≠0

отрезок на осях OY:

$b =  — \frac{D}{B}$, B≠0

отрезок на осях OZ:

$c =  — \frac{D}{C}$, C≠0

 

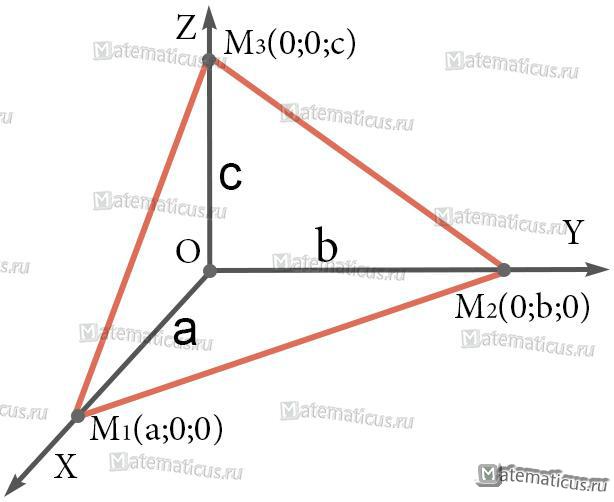
На рисунке точки M₁(a; 0; 0), M₂(0; b; 0) и M₃(0; 0; c) являются точками пересечения плоскости с координатными осями

Примечание

Плоскость, проходящую через начало координат, нельзя представить уравнением в отрезках

---

  Пример
Написать уравнение плоскости  4x-6y+z-12=0  в отрезках.

$a =  — \frac{-12}{4}$, $b =  — \frac{-12}{-6}$,  $c =  — \frac{-12}{1}$

Находим a=3, b=−2, c=12.
Уравнение в отрезках есть:

$\frac{x}{3} + \frac{y}{{ — 2}} + \frac{z}{{12}} = 1$