Уравнение плоскости, проходящей через точку перпендикулярно к прямой

Плоскость, проходящая через данную точку М₀(х₀; у₀; z₀) и перпендикулярная к данной прямой:

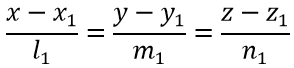
имеет нормальный вектор N{ι₁, m₁, n₁} и представляется уравнением:

   l₁(x-x₁) + m₁(y-y₁) + n₁(z-z₁)=0

или в векторной форме:

   a₁(r−r₀)=0

---

Пример
Плоскость, проходящая через точку (9; -3; 7) и перпендикулярная к прямой:

$\frac{x}{0} = \frac{y}{4} = \frac{{z — 3}}{4}$

, представляется уравнением:

  4⋅(у+3)+4⋅(z-7)=0
4у+4z−16=0