Углом между двумя пересекающимися прямыми в пространстве называется наименьший из углов, образованный лучами этих прямых с вершиной в точке их пересечения.
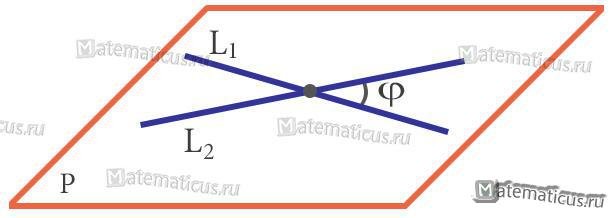
Угол φ между прямыми L1 и L2 находится по формуле
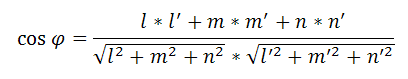
где l, m, n и l’, m’, n’— направляющие коэффициенты прямых L1 и L2.
Пример
Найти угол между прямыми
$\left\{ {\begin{array}{*{20}{c}}{2x — 2y — z + 7 = 0} \\ {x + 2y — 2z + 3 = 0}\end{array}} \right.$
$\left\{ {\begin{array}{*{20}{c}} {4x + y + 3z — 5 = 0} \\ {2x + 2y — 3z + 10 = 0} \end{array}} \right.$
Решение
Направляющие коэффициенты первой прямой равны (смотрите пример) ι=2, m=1, n=2, а направляющие векторы второй прямой равны −9, 18, 6, разделив их на 3, получим ι=−3, m= 6, n=2.
Имеем:
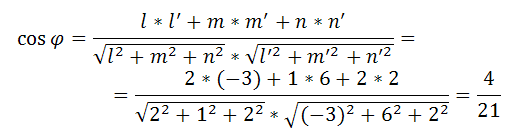
Откуда находим, arccosφ=4/21
φ=790.02
