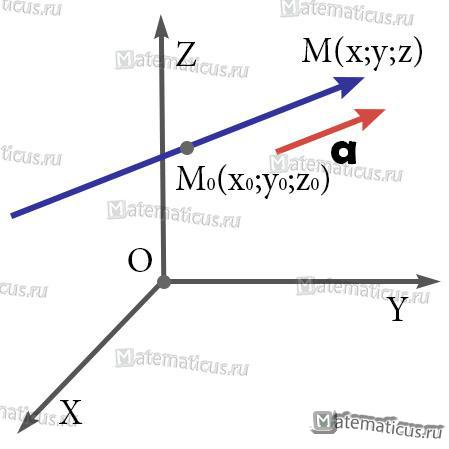
Прямая, проходящая через точку М₀(х₀; у₀; z₀), параллельная направляющему вектору

а{l, m, n} (подробно об этом векторе), представляется уравнениями:

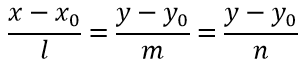
выражающими коллинеарность векторов а{l, m, n} и

 $\overrightarrow {{M_0}M}  = \left\{ {x — {x_0},y — {y_0},z — {z_0}} \right\}$

Это уравнения  называются каноническими (симметричными) уравнением прямой.

---

Пример 
Симметричные уравнения прямой, проходящей через точки М₀(4; 0; 5), М₁(4; 2; 9), будут:

$\frac{{x — 4}}{0} = \frac{{y — 0}}{2} = \frac{{z — 5}}{4}$

Выражение  $\frac{{x — 4}}{0}$  условно,  оно означает x-4=0, так что надо писать так:

$x = 4,\frac{y}{2} = \frac{{z — 5}}{4}$

  Прямая М₀М₁ перпендикулярна к оси ОХ, так как ι=0.

---

Приведение уравнений прямой к симметричному виду

Для того чтобы привести уравнения прямой

  A₁x + B₁y + C₁z + D₁=0  (1) 
      A₂x + B₂y + C₂z + D₂=0  (2) 

к симметричному виду, надо определить координаты x₀, y₀, z₀ какой-либо точки, лежащей на прямой и направляющие коэффициенты l, m, n.

---

Пример 

Привести к симметричному виду уравнения:

  x+2y-3z-2=0,    -3x+4y-6z+21=0

Зададим координате у или z какое-либо значение (координате х произвольное значение задать нельзя, так как уравнение будет несовместимым в этом случае); например, пусть у=0, тогда получим точку М₀(5; 0; 1).
Найдём направляющие коэффициенты:

$l = \left| {\begin{array}{*{20}{c}} 2&{ — 3} \\ 4&{ — 6} \end{array}} \right|=$

$ = 2\cdot\left( { — 6} \right) — 4\cdot\left( { — 3} \right) = 0$

$m = \left| {\begin{array}{*{20}{c}}{ — 3}&1 \\ { — 6}&{ — 3} \end{array}} \right| = $

$=\left( { — 3} \right)\cdot\left( { — 3} \right) — \left({ — 6} \right)\cdot1 = 15$

$n = \left| {\begin{array}{*{20}{c}}1&2 \\ { — 3}&4 \end{array}} \right| =$

$ =1\cdot4 — \left( { — 3} \right)\cdot2 = 10$

Направляющие коэффициенты будут l=0, m=15, n=10 или (помноженная на 1/5),
получаем l=0, m=3, n=2
Получаем симметричные уравнения:

 $\frac{{x — 2}}{0} = \frac{y}{3} = \frac{{z — 1}}{2}$