Угол между двумя плоскостями

Пусть даны две плоскости

  A₁x+B₁y+C₁z+D₁=0 и A₂x+B₂y+C₂z+D₂=0

Эти плоскости образуют четыре двугранных угла, которые попарно равны. Один из них равен углу между нормальными векторами (нормалями) N₁{A₁;B₁;C₁} и N₂{A₂;B₂;C₂}. Допустим, обозначим один из четырех двугранных углов символом φ (см. рисунок ниже)

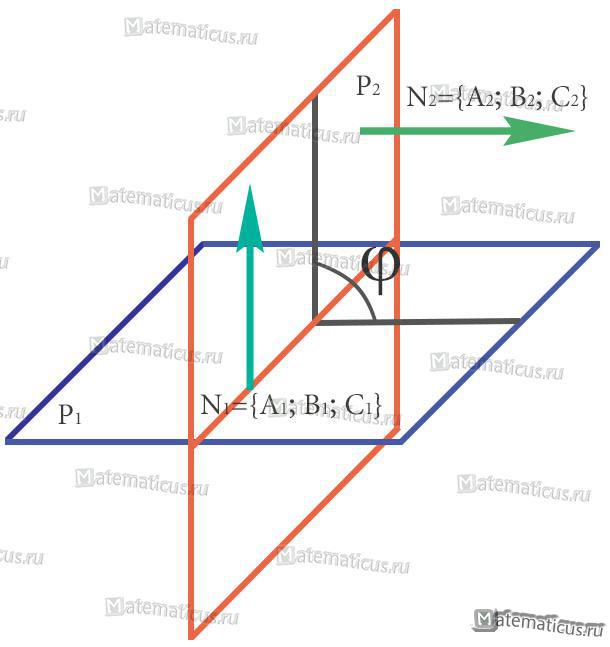
Получим формулу, которая определяет угол между двумя плоскостями:

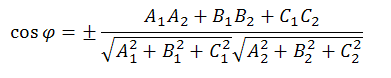
или

$\cos \varphi  =  \pm \frac{{{{\vec N}_1}\cdot{{\vec N}_2}}}{{\left| {{{\vec N}_1}} \right|\cdot|{{\vec N}_2}|}}$

Величина двугранного угла между плоскостями принадлежит промежутку от 0° до 180°.

Если выбираем положительный знак, то получаем cos(N₁,^{^}N₂), а если отрицательный, то получаем cos[180⁰ — (N₁,^{^}N₂)]

---

Пример 
Заданы уравнения двух плоскостей
$x — y + \sqrt 2 z — 7 = 0$  и  $x + y + \sqrt 2 z + 5 = 0$

Требуется найти угол между плоскостями

Решение
Подставляя в формулу для нахождения угла между двумя плоскостями, получаем

$\cos \varphi  =  \pm \frac{{1\cdot1 + \left( { — 1} \right)\cdot1 + \sqrt 2 \cdot\sqrt 2 }}{{\sqrt {{1^2} + {{\left( { — 1} \right)}^2} + {{\left( {\sqrt 2 } \right)}^2}} \sqrt {{1^2} + {1^2} + {{\left( {\sqrt 2 } \right)}^2}} }} =$

$=  \pm \frac{1}{2}$

φ=arccos$\pm \frac{1}{2}$

Отсюда получаем угол φ=60⁰ или φ=180⁰ − 60⁰=120⁰

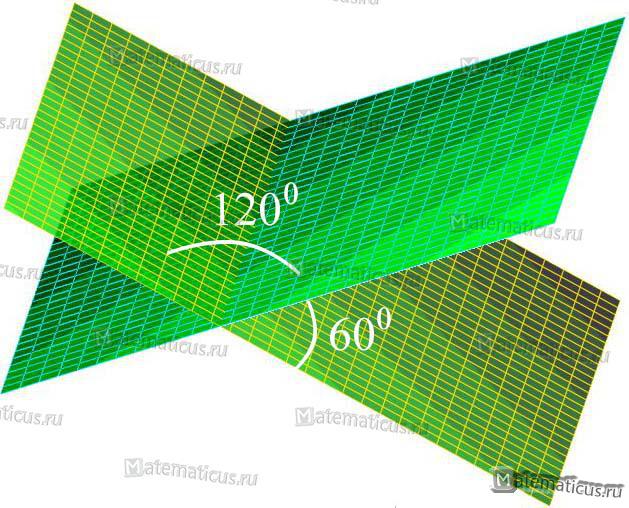
На рисунке отмечены полученные углы между этими плоскостями