Расстоянием d от точки M0(x0; y0; z0) до плоскости p: Ax + By + Cz + D = 0 в пространстве называется длина перпендикуляра, опущенного из данной точки на данную плоскость и равно:
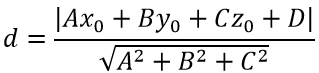
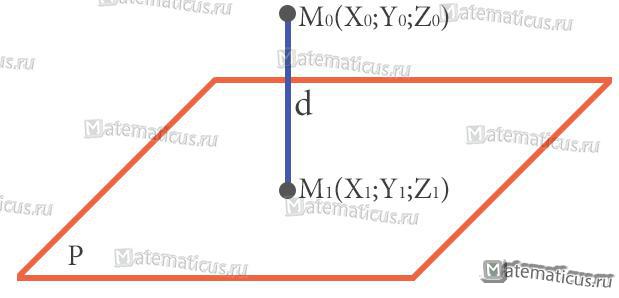
Точка M1(x1; y1; z1) основание перпендикуляра, опущенного из точки M0(x0; y0; z0) на плоскость P.
На рисунке это расстояние равно:
d=|M1M0|
Пример
Найти расстояние от точки M0(2; 4; 3) до плоскости 2x-y+z-4=0
Решение
Здесь x0=2, y0=4, z0=3, A=2, B=-1, C=1. Подставляя в формулы выше, получаем решение
$d = \frac{{\left| {2\cdot2 + \left( { — 1} \right)\cdot4 + 1\cdot3 + \left( { — 4} \right)} \right|}}{{\sqrt {{2^2} + {{\left( { — 1} \right)}^2} + {1^2}} }} = \left| {\frac{{ — 1}}{{\sqrt 6 }}} \right| = \frac{1}{{\sqrt 6 }}$
