Углы α, β, γ образуемые прямой L
A1x+B1y+C1z+D1=0 (1)
A2X+B2y+C2Z+D2=0 (2)
A2X+B2y+C2Z+D2=0 (2)
(в одном из двух ее направлений) с осями координат, находятся из соотношений:
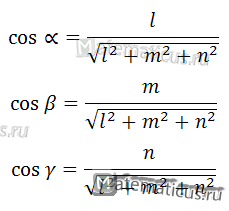
где l, m, n — направляющие коэффициенты прямой L.
Величины cosα , cosβ, cosγ называются направляющими косинусами прямой L.
Пример
Найти углы, образуемые прямой 2x-2y-z+8=0, x+2y-2z+1=0 с осями координат
Решение
Находим направляющие коэффициенты данной прямой
$\vec N_1 \times \vec N_2 = \left| {\begin{array}{*{20}{c}} {\vec i}&{\vec j}&{\vec k} \\ 2&{ — 2}&{ — 1} \\ 1&2&{ — 2} \end{array}} \right| =$
$=6i — 3j + 6k$
можно принять (похожий пример) ι=6, m=3, n=6
Подставляя значения в формулу выше, получаем:
cosα=6/9=2/3,
cosβ=3/9=1/3,
cosγ=6/9=2/3
Отсюда
α≈480, β≈700, γ≈480
