Пересечение прямой и плоскости

Прямая K, образованная уравнениями двух пересекающихся плоскостей

А₁х+В₁у+С₁z+D₁=0

  А₂х+В₂у+C₂z+D₂=0  

и плоскость P

  Аx+Ву+Сz+D=0 

могут не иметь ни одной общей точки при условии если прямая K параллельна плоскости Р, также могут иметь бесчисленное множество общих точек если прямая K лежит на плоскости Р или иметь только одну общую точку. Вопрос сводится к разысканию общих точек трех плоскостей.

Примечание

Плоскость на рисунках обозначена сплошным синим цветом.

---

  Пример 1
Прямая x+y+z-1=0, x-2y-3z-5=0 не имеет общих точек с плоскостью 2x-y-2z-8=0 (они параллельны)

---

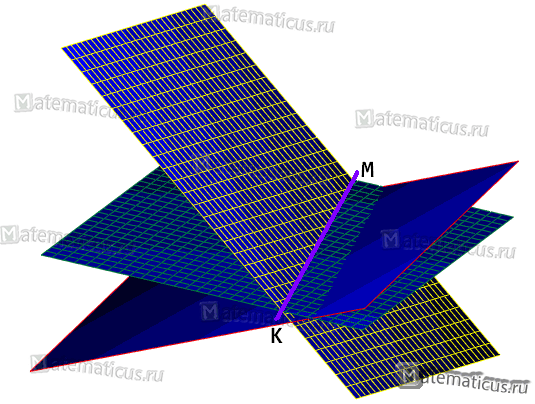
Пример 2 
Прямая x-2y-3z-5=0, 2x-y-2z-6=0 лежит в плоскости x+y+z-1=0

---

Пример 3
Прямая x+y-z+2=0, х-у+2=0 пересекается с плоскостью х+2у-1=0 в точке
(-1; 1; 2). На рисунке точка обозначена желтым цветом.