Проекции прямой на координатные плоскости

Если прямая представляется уравнениями

 A₁x + B₁y + C₁z + D₁=0  (1) 
     A₂x + B₂y + C₂z + D₂=0  (2) 

,где С₁ и С₂ одновременно не равны нулю (случай когда С₁=С₂= 0 рассмотрен ниже в примере 2). Чтобы найти проекцию прямой на плоскость XOY, необходимо исключить z из уравнений (1) и (2). Полученное уравнение (вместе с уравнением z=0) будет представлять искомую проекцию. Аналогично находятся проекции на плоскости для YOZ и ZOX.

---

Пример 1
Найти проекцию прямой L

2x+4y-3z-12=0

        x-2у+4z-10=0       

на плоскость ХОY.

Решение
Для того, чтобы исключить z, умножим первое уравнение на 4, а второе — на 3 и затем сложим. Получим:

4⋅(2x+4y-3z-12)+3⋅(x-2y+4z-10)=0
11x+10у-78=0

Это уравнение вместе с уравнением z=0 представляет проекцию L’ прямой L на плоскость XOY.

---

Пример 2 
Найти проекции прямой L
2х-3у=0
х+у-4=0
на координатные плоскости.

  Решение

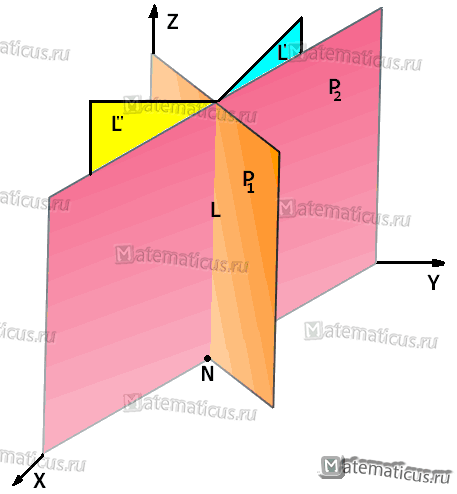
В данных уравнениях отсутствует z, потому что плоскости Р₁ и Р₂ перпендикулярны (Р₁⊥Р₂) к плоскости XOY. Прямая L перпендикулярна к XOY и проектируется на плоскость XOY в точку N с координатой z_N=0. Решая систему, находим значения x_N=12/5, у_N=8/5.
Уравнение проекции L’ на плоскость YOZ можно найти по общему способу, исключая х из уравнения. Получим у=8/5, то есть то же равенство, которое найдено выше для у_N. Уравнение проекции L» на плоскость XOZ будет x=12/5