Смешанным произведением трех векторов а, b, с называется скалярное произведение вектора а на векторное произведение b×с, т. е. а⋅(b×с) или (b×с)⋅а
Обозначение: аbс
Выразим смешанное произведение через координаты трех векторов a={ax;ay;az}, b={bx;by;bz} и c={cx;cy;cz}, получим формулу, которая равна определителю матрицы третьего порядка:
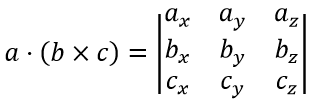
или
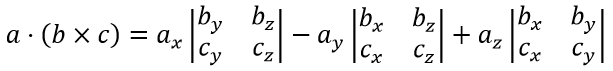
Признаком компланарности смешанного произведения векторов abc является обращение в ноль модуля смешанного произведения abc, т.е.
|abc|=0
Пример
Доказать, что векторы a=(1;-1;2), b=(1;2;-1) c=(2;-2;4) являются компланарными
Решение
|abc|=$\left| {\begin{array}{*{20}{c}}1&{ — 1}&2 \\1&2&{ — 1} \\2&{ — 2}&4\end{array}} \right| = $
$ = 1\cdot\left| {\begin{array}{*{20}{c}}2&{ — 1} \\ { — 2}&4 \end{array}} \right| — \left( { — 1} \right)\cdot\left| {\begin{array}{*{20}{c}}1&{ — 1} \\ 2&4 \end{array}} \right| + 2\cdot\left| {\begin{array}{*{20}{c}}1&2 \\ 2&{ — 2} \end{array}} \right| = $
$ = 1\cdot\left( {2\cdot4 — \left( { — 1} \right)\cdot\left( { — 2} \right)} \right) — \left( { — 1} \right)\cdot\left( {1\cdot4 — \left( { — 1} \right)\cdot2} \right) + 2\cdot\left( {1\cdot\left( { — 2} \right) — 2\cdot2} \right) = 0$
Так как |abc| = 0, следовательно векторы компланарны. Что и требовалось доказать.
Свойства смешанного произведения векторов
1.
abc = bса = cab = − (bас) = − (cba) = − (acb)
2. Свойство распределительности
(a+b)cd = acd+bcd
3. Cвойство сочетательности
(mа) bс = m (аbс)
4. Смешанное произведение равно нулю, если:
— два из векторов коллинеарны;
— имеющее хотя бы два равных сомножителя, т.е. (aab=0);
— хотя бы один из векторов равен нулю;
— векторы компланарны.
Геометрический смысл смешанного произведения векторов
Объём параллелепипеда, построенного на трех векторах равен модулю смешанного произведения векторов. Тогда запишем формулу
Vпараллелепипеда=|аbс|
Пример расчёта объёма параллелепипеда, построенного на трех векторах см. здесь.
Объём треугольной призмы, построенной на трех векторах равен половине модуля смешанного произведения векторов. Формула примет вид:
Vтреугольной призмы=$\frac{1}{2}$⋅|аbс|
Вычисляется аналогично, как и объёма параллелепипеда, только делится пополам.
Объём треугольной пирамиды, построенной на трех векторах равен 1/6 модуля смешанного произведения векторов. Получаем формулу:
Vтреугольной пирамиды=$\frac{1}{6}$⋅|аbс|
Пример вычисления объём треугольной пирамиды см. здесь
