Выражение проекция вектора на прямую употребляется в двух разных смыслах: геометрическом и алгебраическом.
Геометрический смысл
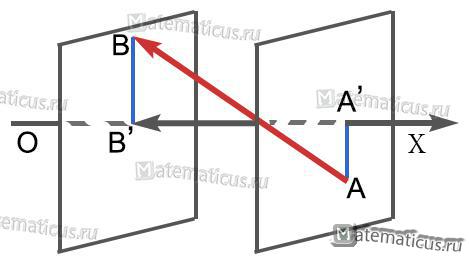
Проекцией (геометрической) вектора $\overrightarrow {AB} $ на ось (прямую) OX называется вектор $\overrightarrow {A’B’} $, начало которого A’ есть проекция начала A на ось (прямую) OX, а конец B’ — проекция конца B на ту же прямую (ось).
Обозначается: Прox$\overrightarrow {AB} $ или $\overrightarrow {AB} $
Алгебраический смысл
Проекцией (алгебраической) вектор $\overrightarrow {AB} $ на ось (прямую) OX называется длина вектора $\overrightarrow {A’B’} $ , взятая со знаком «+» или «−», смотря по тому, имеет ли вектор $\overrightarrow {A’B’} $ то же направление, что ось OX (вектор с).
Обозначается: прox $\overrightarrow {AB} $ или прс $\overrightarrow {AB} $
Примечание
Геометрическая проекция вектора есть вектор, а алгебраическая проекция вектора есть число.
Пример 1
Геометрическая проекция вектора $\overrightarrow {OK} $ =a
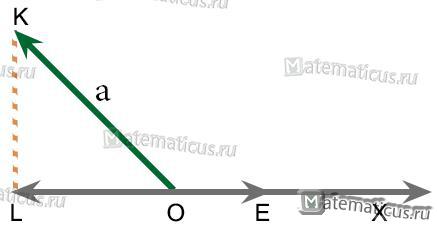
на ось OX есть вектор $\overrightarrow {OL} $. Его направление противоположно направлению оси X, а длина (при единице масштаба OD) равна 2. Значит алгебраическая проекция вектора $\overrightarrow {OK} $ на ось OX есть отрицательное число -2.
Пр$\overrightarrow {OK} $ = $\overrightarrow {OL} $, пр$\overrightarrow {OL} $=-2.
Основные теоремы о проекциях вектора
1) Проекция суммы векторов на какую-либо ось равна сумме проекций слагаемых векторов на ту же ось.
Пр (a1+a2+a3)=Пр a1+Пр a2+Пр a3
Пример 2
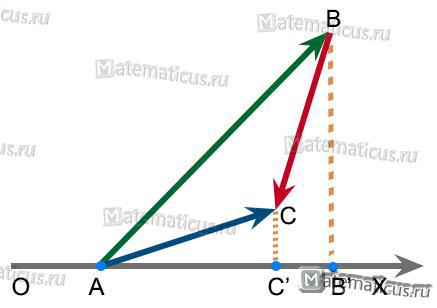
Вектор $\overrightarrow {AC} $ есть сумма векторов $\overrightarrow {AB} $ и $\overrightarrow {BC} $. Геометрическая проекция вектора $\overrightarrow {AC} $ на ось ОX есть вектор $\overrightarrow {AC’} $, а геометрические проекции векторов $\overrightarrow {AB} $ и $\overrightarrow {BC} $ суть $\overrightarrow {AB’} $ и $\overrightarrow {B’C’} $. при этом $\overrightarrow {AC’} $=$\overrightarrow {AB’} $+$\overrightarrow {B’C’} $, так что Пр($\overrightarrow {AB} $+$\overrightarrow {BC} $)=Пр$\overrightarrow {AB} $+Пр$\overrightarrow {BC} $
Пример 3
Пусть OE есть единица масштаба; тогда алгебраическая проекция вектора
$\overrightarrow {AB} $ на ось OX равна 4 (длина $\overrightarrow {AB’} $ взята со знаком плюс), т. е. пр$\overrightarrow {AB} $=4.
Далее пр$\overrightarrow {BC} $=-2 (длина $\overrightarrow {B’C’} $, взятая со знаком минус) и пр$\overrightarrow {AC} $=+2 (длина $\overrightarrow {AC’} $, взятая со знаком плюс).
Имеем пр$\overrightarrow {AB} $ +пр$\overrightarrow {BC} $=4-2=2;
с другой стороны пр($\overrightarrow {AB} $ +$\overrightarrow {BC} $)=пр$\overrightarrow {AC} $=2
2) Алгебраическая проекция вектора на какую-либо ось равна произведению длины вектора на косинус угла между осью и вектором:
прab=|b|⋅cos(a,^b)
Пример 4
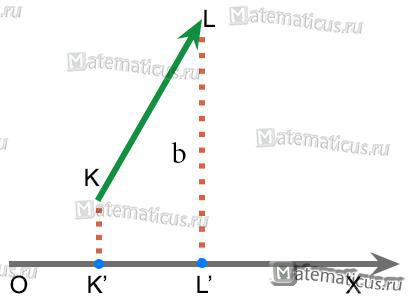
Вектор b=$\overrightarrow {KL } $ образует с осью OX угол 600, если |b|=4, так что
прab=|b|·cos(a,^b) =4·cos600=4·1/2=2
