Псевдосфера — это поверхность отрицательной Гауссовой кривизны, которая имеет форму, аналогичную сфере, но в гиперболическом пространстве. Она является аналогом геометрической сферы в гиперболической геометрии, подобно тому, как плоскость является аналогом сферы в евклидовой геометрии.
Псевдосферы также широко изучались в математике и физике, особенно в контексте гиперболической геометрии и теории кривых поверхностей. Они имеют уникальные свойства и играют важную роль в понимании гиперболических пространственных структур.
Истолкование итальянского математика Бельтрами о псевдосфере 1868 г. в научной работе «Опыт интерпретации неевклидовой геометрии»:
Псевдосфера пример поверхности с постоянной отрицательной кривизной, которая является первой реальной моделью неевклидовой геометрии (геометрии Лобачевского).
Псевдосферу можно получить вращением линии трактрисы вокруг ее оси.
Название псевдосферы вел Бельтрами.
Параметрическое уравнение псевдосферы имеет вид:
x=a·sinu·cosv
y=a·sinu·sinv
z=a·(ln(tg(u/2))+cosu)
График псевдосферы
Площадь псевдосферы определяется по формуле:
S=4πa2
Формула объёма псевдосферы:
V=2/3πa3
Свойство псевдосферы
На псевдосфере, которая является примером геометрии с отрицательной кривизной, сумма углов в треугольнике будет меньше 180 градусов, в отличие от евклидовой геометрии, где сумма углов в треугольнике равна 180 градусам, и гиперболической геометрии, где сумма углов в треугольнике больше 180 градусов.
На псевдосфере сумма углов в треугольнике зависит от его размера и формы, но всегда будет меньше 180 градусов. Это связано с тем, что геометрия псевдосферы имеет отрицательную кривизну, что приводит к изменению свойств прямых и углов в сравнении с классической евклидовой геометрией.
Гауссова кривизна псевдосферы равна −1/a²

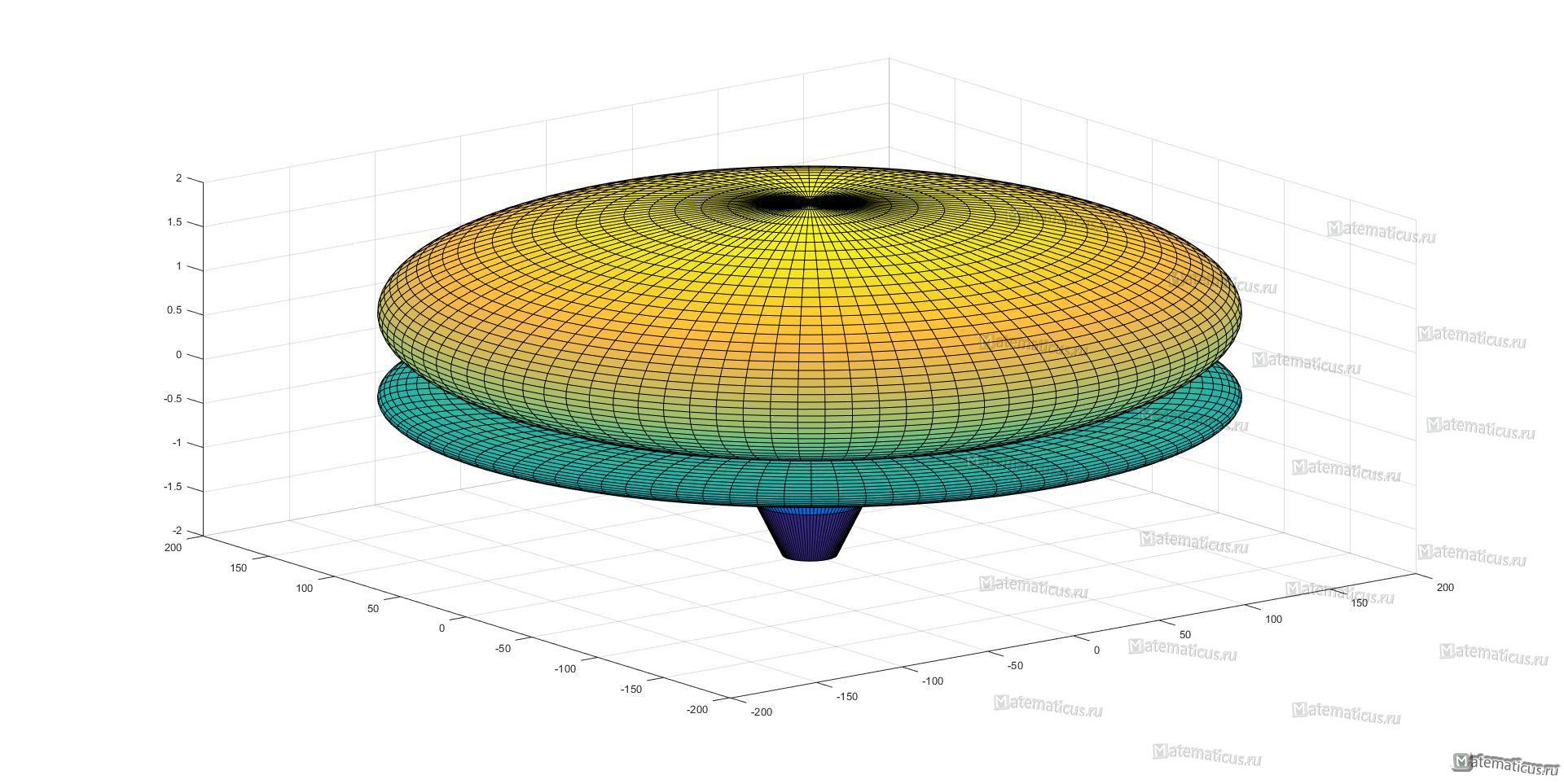
Где вы видите «плоскости»? Сумма углов меньше 180, так как не плоскости. а поверхность обладает отрицательной кривизной.
Спасибо Вам! Исправили описку — плоскость на поверхность.