Прямоугольными координатами a называются алгебраические проекции вектора a на оси координат.

Координаты вектора обозначаются большими буквами X, Y, Z (координаты точки- малыми.)

  Запись координат: a{X,Y,Z} или a={X,Y,Z }

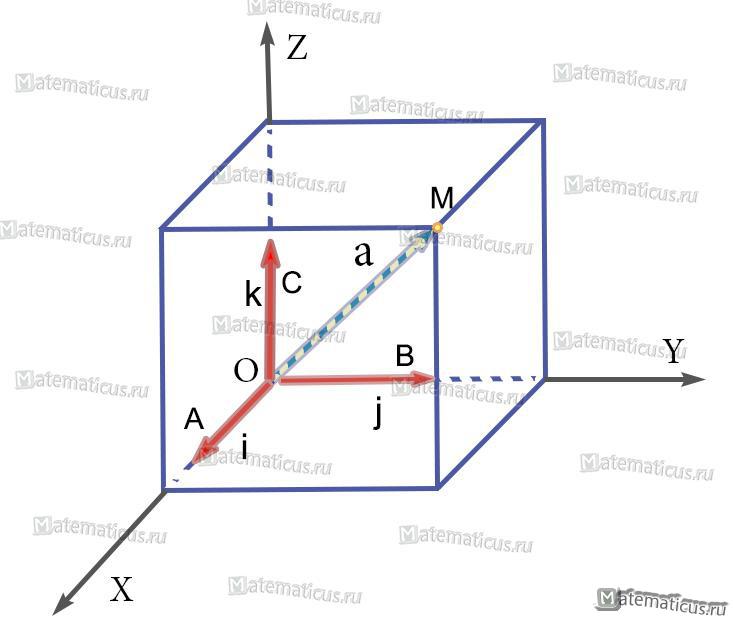
Допустим, если X=2 –абсцисса, Y=3 – ордината, Z=4 — аппликата, то запись примет вид: $\overrightarrow {OM} $={2,3,4}

Каждый вектор a равен сумме произведений трёх основных векторов на соответствующие координаты вектора a:

  a=X⋅i+Y⋅j+Z⋅k 

В качестве примера, имеем следующее уравнение:
$\overrightarrow {OM} $=2i+3j+4k

  Действие над векторами 

При сложении векторов их координаты складываются:

   a=a₁+a₂, т. е. X=X₁+X₂, Y=Y₁+Y₂, Z=Z₁+Z₂ 

  При вычитании векторов их координаты определяются:

  a=a₂-a₁, т. е. X=X₁−X₂, Y=Y₁−Y₂, Z=Z₁−Z₂ 

  При умножении векторов на число все координаты множатся, если:

  m₂=λ⋅m₁, то X₂=λ⋅X₁, Y₂= λ⋅Y₁, Z₂= λ⋅Z₁ 

  При делении векторов на число все координаты делятся, если:

${m_2} = \frac{{{m_1}}}{\lambda }$, т. е. ${X_2} = \frac{{{X_1}}}{\lambda },{Y_2} = \frac{{{Y_1}}}{\lambda },{Z_2} = \frac{{{Z_1}}}{\lambda }$

Модуль вектора в пространстве определяется:

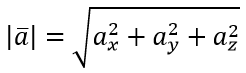
где

Координаты вектора в пространстве a{a_x; a_y; a_z;} находятся по формулам:

a_x = X₂ — X₁

a_y = Y₂ — Y₁

a_z = Z₂ — Z₁