Полярным расстоянием плоскости LMN называется длина р перпендикуляра ОК, проведенного к плоскости из начала О. 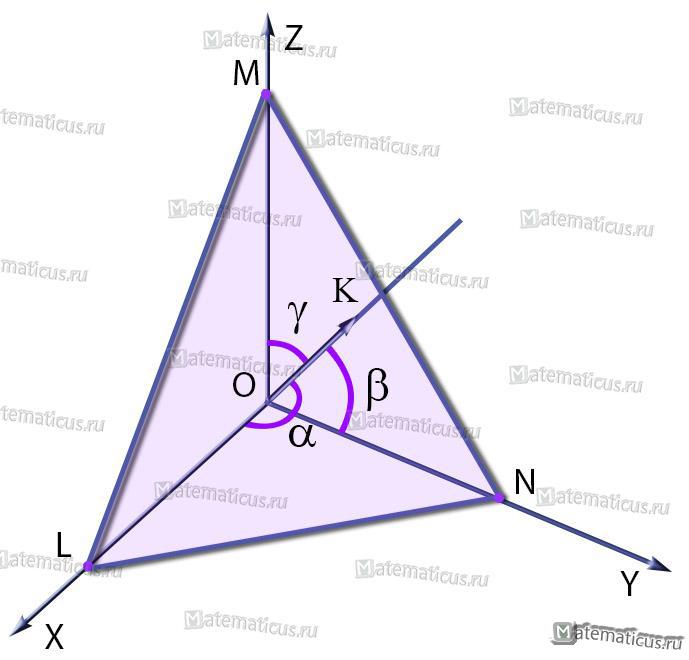
Примечание
Полярное расстояние положительно или равно нулю.
Полярными углами плоскости LMN называются углы: α=∠LОК, β=∠NOK, γ=∠MOK
между положительным направлением прямой ОК и осями координат (эти углы считаются положительными и не превосходящими 180°).
Углы α, β, γ связаны соотношением:
cos2α + cos2β + cos2γ = 1
Полярное расстояние р и полярные углы α, β, γ называются полярными параметрами плоскости LMN.
Если плоскость LMN дана уравнением Ах + Ву + Cz + D=0, то ее полярные параметры определяются формулами:
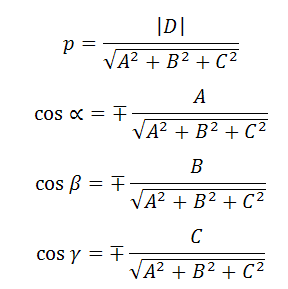
где знаки «минус» берутся, когда D>0, и «плюс», когда D<0. Если же D=0, то знак берется произвольно.
Если плоскость LMN дана уравнением Ах + Ву + Cz + D=0, то ее полярные параметры определяются формулами:
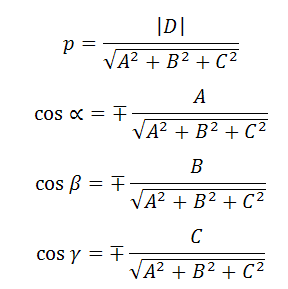
где знаки «минус» берутся, когда D>0, и «плюс», когда D<0. Если же D=0, то знак берется произвольно.
Пример
Найти полярные параметры плоскости x-2y+2z-3=0 (здесь А=1, В =-2, С = 2, D = -3).
Решение
Здесь нужно взять знак «плюс», так как D=-3<0, тогда
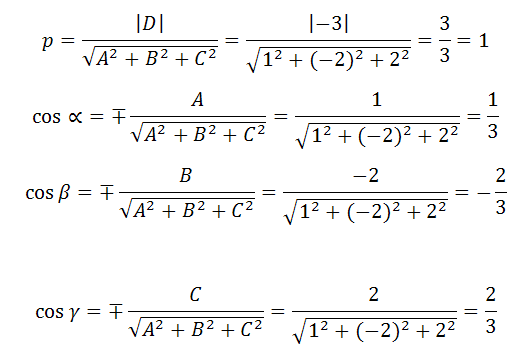
следовательно получаем,
p=1, α≈70,530, β≈131,810, γ ≈48,190
