Условие перпендикулярности плоскостей

 

Объём параллелепипеда построенного на векторах

Объём параллелепипеда, построенного на трех векторах

a₁={X₁;Y₁;Z₁}, a₂={X₂;Y₂;Z₂} и a₃={X₃;Y₃;Z₃} равен модулю смешанного произведения векторов и  находится по формуле:

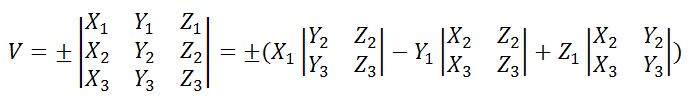
где координаты векторов в соответствии с рисунком

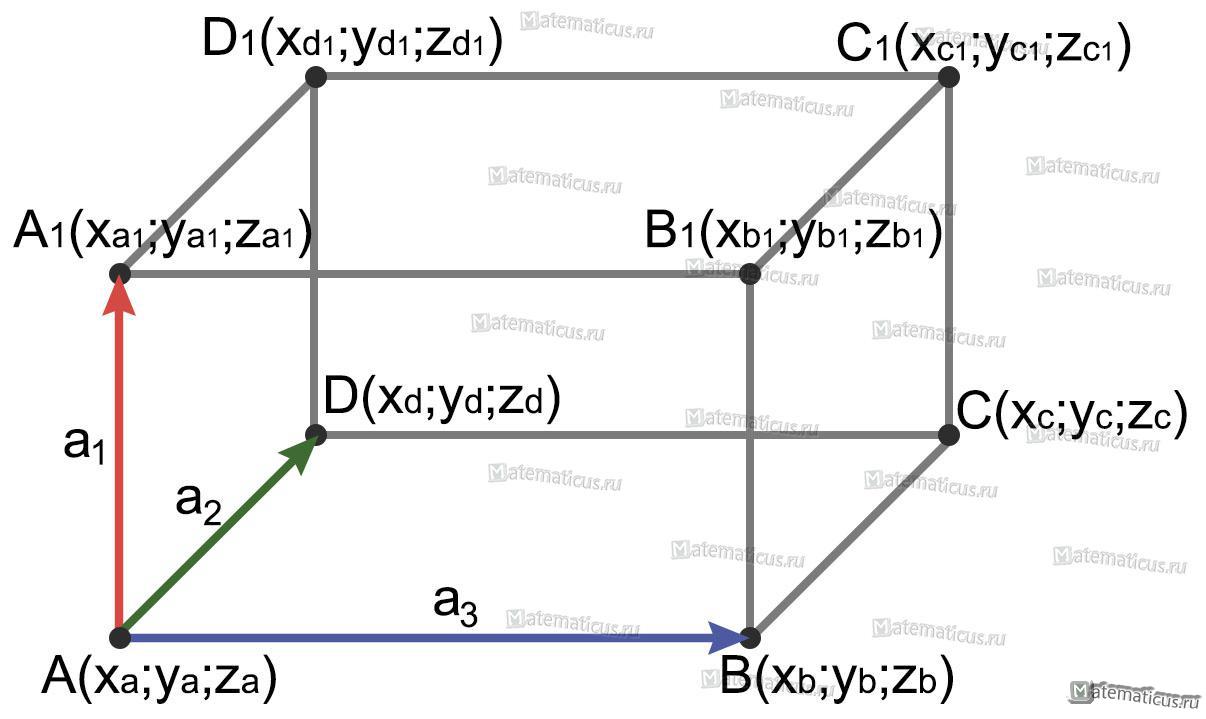
вычисляются следующим образом

a₁=$\overrightarrow {AA_1} $={X₁=X_a1-X_a; Y₁=Y_a1-Y_a; Z₁=Z_a1-Z_a; }

a₂=$\overrightarrow {AD} $={X₂=X_d-X_a; Y₂=Y_d-Y_a; Z₂=Z_d-Z_a; }

a₃=$\overrightarrow {AB} $={X₃=X_b-X_a; Y₃=Y_b-Y_a; Z₃=Z_b-Z_a; }

  Знак плюс берется, когда определитель третьего порядка положителен, а минус наоборот – знак отрицателен.

Пример

  Найти объём параллелепипеда, построенного на векторах a₁={2;3;2}, a₂={-1;-4;3} и a₃={3;1;2}

Решение

$V =  \pm \left| {\begin{array}{*{20}{c}}2&3&2 \\  { — 1}&{ — 4}&3 \\ 3&1&2 \end{array}} \right| =  $

$=\pm \left( {2\left| {\begin{array}{*{20}{c}} { — 4}&3 \\ 1&2 \end{array}} \right| — 3\left| {\begin{array}{*{20}{c}}{ — 1}&3 \\ 3&2 \end{array}} \right| + 2\left| {\begin{array}{*{20}{c}}{ — 1}&{ — 4} \\ 3&1 \end{array}} \right|} \right) = $

$ =  \pm \left( {2\cdot\left( {\left( { — 4} \right)\cdot2 — 1\cdot3} \right) — 3\left( {\left( { — 1} \right)\cdot2 — 3\cdot3} \right) + 2\left( {\left( { — 1} \right)\cdot1 — 3\cdot\left( { — 4} \right)} \right)} \right) = -33$

  Так как определитель отрицателен, берем перед ним знак «—».

Тогда объём параллелепипеда равен  V=33