Всякая прямая линия KM представляется системой двух уравнений:
А1х+В1у+С1z+D1=0 (1)
А2х+В2у+C2z+D2=0 (2)
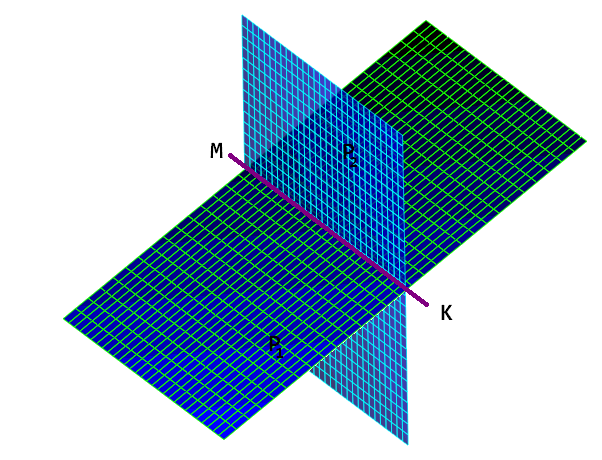
представляющих (если их рассматривать по отдельности) какие-либо две (различные) плоскости P1 и Р2, проходящие через KM. Уравнения (1) и (2) (взятые в совокупности) называются уравнениями прямой KM.
Условие, при котором два уравнения первой степени представляют прямую
Система
А1х+В1у+С1z+D1=0
А2х+В2у+C2z+D2=0
представляет прямую линию.
Если коэффициенты A1, B1, С1 не пропорциональны коэффициентам A2, B2, С2 (в этом случае плоскости (1) и (2) не параллельны).
Если коэффициенты A1, B1, С1 пропорциональны коэффициентам A2, B2, С2, но свободные члены не подчинены той же пропорции:
A1:A2=B1:B2=С1:С2≠D1: D2
, то система несовместна и не представляет никакого геометрического образа (плоскости (1) и (2) параллельны и не совпадают).
Если все четыре величины A1, B1, С1, D1 пропорциональны величинам
A2, B2, С2, D2:
A1:A2=B1:B2=С1:С2=D1: D2
, то одно из уравнений (1), (2) есть следствие другого и система представляет плоскость (плоскости (1) и (2) совпадают).
Пример 1
Система
4x-3y+10z-4=0, 8x-6у+40z-8=0
представляет прямую линию (во втором уравнении коэффициенты А и В вдвое больше, чем в первом, а коэффициент С — вчетверо).
Пример 2
Система
4x-3y+10z-4=0, 8x-6у+20z-8=0
представляет плоскость (все четыре величины А, В, С, D пропорциональны).
Пример 3
Система
4x-3y+10z-4=0, 8x-6у+20z-12=0
не представляет никакого геометрического образа (величины А, В, С пропорциональны, a D не подчинена той же пропорции; система несовместна).
