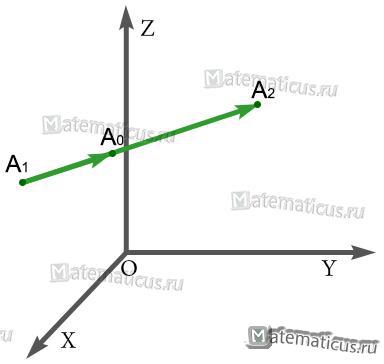
Деление отрезка в данном отношении в пространстве определяется следующими уравнениями

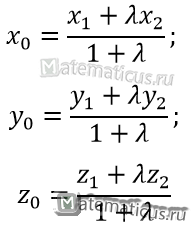
Данные уравнения получаются следующим образом

Пусть даны две точки A₁(x₁, y₁,z₁) и A₂(x₂, y₂,z₂).

Требуется найти координаты точки A₀(x₀, y₀,z₀), делящей отрезок в отношении λ, т.е.

$\frac{{\overrightarrow {{A_1}{A_0}} }}{{\overrightarrow {{A_0}{A_2}} }} = \lambda $ или $\overrightarrow {{A_1}{A_0}}  = \lambda \overrightarrow {{A_0}{A_2}} $

$\overrightarrow {{A_1}{A_0}}  = \left( {{x_0} — {x_1},{y_0} — {y_1},{z_0} — {z_1}} \right)$

$\overrightarrow {{A_0}{A_2}}  = \left( {{x_2} — {x_0},{y_2} — {y_0},{z_2} — {z_0}} \right)$

${x_0} — {x_1} = \lambda \left( {{x_2} — {x_0}} \right)$

${z_0} — {z_1} = \lambda \left( {{z_2} — {z_0}} \right)$

${z_0} — {z_1} = \lambda \left( {{z_2} — {z_0}} \right)$

Отсюда получаем исходные уравнения, т.е.

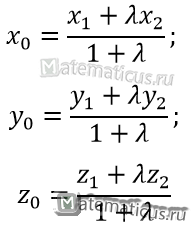
Деление отрезка в данном отношении на плоскости см. здесь

---

Рассмотрим ещё один из способов деления отрезка в данном отношении в пространстве.

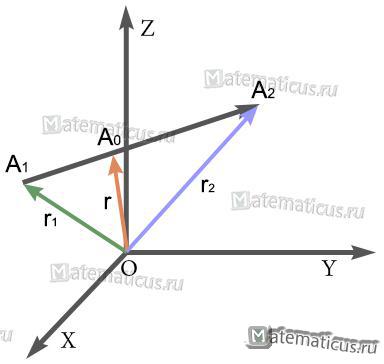
Пусть радиус-вектор r точки A₀, делящий отрезок А₁А₂ в отношении А₁А₀:А₀А₂=m₁:m₂ определяется формулой:

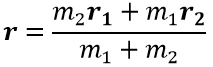
где r₁  и r₂ — радиус-вектор точек А₁  и А₂

Координаты точки A₀ находятся по формулам

${x_0} = \frac{{{m_2}{x_1} + {m_1}{x_2}}}{{{m_1} + {m_2}}},$

${y_0} = \frac{{{m_2}{y_1} + {m_1}{y_2}}}{{{m_1} + {m_2}}},$

${z_0} = \frac{{{m_2}{z_1} + {m_1}{z_2}}}{{{m_1} + {m_2}}}$

---

Координаты середины отрезка в пространстве

В частности координаты середины отрезка А₁А₂ в пространстве определяются уравнениями:

---

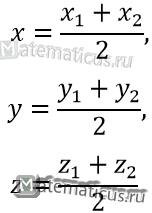
Пример

Найти координаты точки А, делящей отрезок А₁А₂ в отношении А₁А:АА₂=2:3, если  A₁{3; 4; -2} и A₂{-6; -1; 3}

Находим

$x = \frac{{{m_2}{x_1} + {m_1}{x_2}}}{{{m_1} + {m_2}}} = \frac{{3\cdot3 + 2\cdot\left( { — 6} \right)}}{{2 + 3}} =  — \frac{3}{5}$

$y = \frac{{{m_2}{y_1} + {m_1}{y_2}}}{{{m_1} + {m_2}}} = \frac{{3\cdot4 + 2\cdot\left( { — 1} \right)}}{{2 + 3}} =  — 2$

$z = \frac{{{m_2}{z_1} + {m_1}{z_2}}}{{{m_1} + {m_2}}} = \frac{{3\cdot\left( { — 2} \right) + 2\cdot3}}{{2 + 3}} = 0$