1.Пусть прямая, проходит через точку T1(x1;y1) и перпендикулярно прямой y=kx+b, тогда её можно представить уравнением (уравнение прямой перпендикулярной данной прямой):
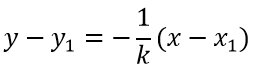
Это и есть уравнение прямой, проходящей через точку перпендикулярно к прямой.
2. Если прямая проходит через ту же точку T1(x1;y1) и перпендикулярно прямой, но только записанной в виде Ax+By+C = 0, то уравнение можно представить как:
A (y − y1) − B (x − x1 ) = 0
Пример 1
Составить уравнение прямой, проходящей через точку L(1;-2) и перпендикулярно прямой
4x-3y-1 = 0 (на рисунке прямая, обозначенная красным цветом)
Решение
Данную прямую можно представить уравнением y = 4/3x-1/3 (здесь a = 4/3). Уравнение искомой прямой есть
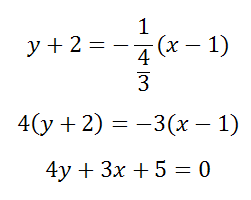
Пример 2
Составить уравнение прямой, проходящей через точку M(-1;-2) и перпендикулярной к прямой 3y+2=0
Решение
Здесь A=0, B=3, получаем 3(x+1)=0, т.е. x+1=0. В этом случае формула неприменима.
