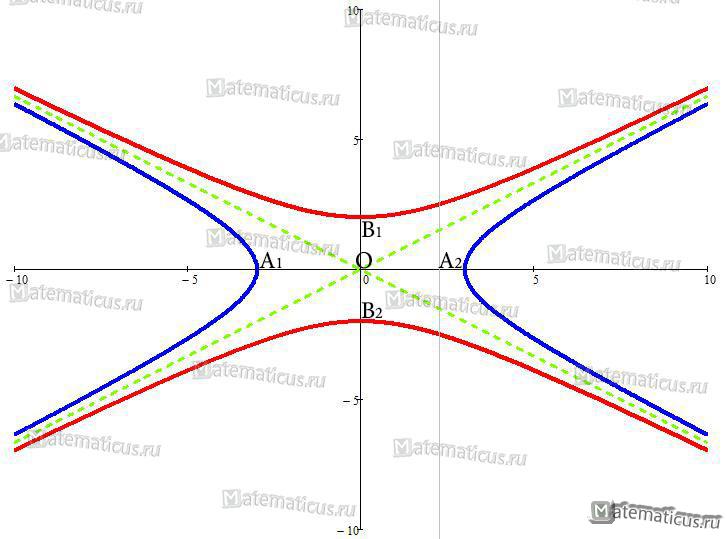
Две гиперболы называются сопряженными, если они имеют общий центр О и общие оси, но действительная ось одной из них является мнимой осью другой, где

A₁A₂ —  действительная ось гиперболы на рисунке ниже синего цвета, но мнимая ось гиперболы красного цвета;

B₁B₂ —  действительная ось гиперболы красного цвета, но мнимая ось гиперболы синего цвета.

Если одна из гипербол представляется уравнением (на рисунке синего цвета)

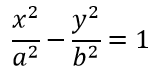
и это есть уравнение одной из сопряженных гипербол, тогда другая представляется уравнением (на рисунке красного цвета)

\[\frac{{{x^2}}}{{{a^2}}} — \frac{{{y^2}}}{{{b^2}}} =  — 1\]

Сопряженные гиперболы имеют общие асимптоты (т.е. асимптоты совпадают) на рисунке обозначено пунктирной зелёной линией.

Уравнение асимптот гиперболы

$y =  \pm \frac{b}{a}x$