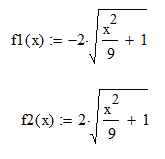Гипербола – геометрическое место точек M, разность расстояний  которых до двух заданных точек F и F’ имеет постоянное значение 2a:

|FM — F’M| = 2a

точки F  и F’ – фокусы гиперболы;

расстояние FF’ – фокусное расстояние и равно FF’=2с;

точка (+a;0) и точка (-a;0) – точки вершины гиперболы.

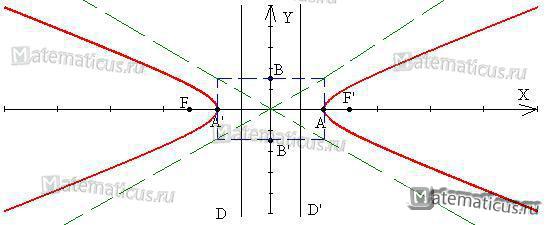
Рисунок 1 — Гипербола

AA’ = 2a – действительная ось гиперболы;

BB’ = 2b – мнимая ось гиперболы;

DD’ — директриса гиперболы, т.е. две прямые заданные линейным уравнением

$x \pm \frac{a}{\varepsilon }$

Директрисы DD’ гиперболы параллельны оси Oу и пересекают ось Ох между вершинами гиперболы.

На рисунке 1 прямые обозначенные пунктирной зеленые линией – это асимптоты гиперболы, т.е. прямые заданные уравнениями

\[y = \frac{b}{a}x\]    и     \[y =  — \frac{b}{a}x\]

называются асимптотами гиперболы

Каноническое уравнение гиперболы

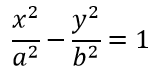
где

c² = a² + b²

Гипербола называется равносторонней (равнобочной), если a=b, тогда уравнение примет вид

x²-y²=a²

Полуоси  a, b и полуфокусное  расстояние c гиперболы выражаются через  следующим образом:

Сопряженная гипербола см. здесь.

Эксцентриситет гиперболы

$\varepsilon  = \frac{c}{a}$

где

ε>1

или

$\varepsilon  = \sqrt {1 + \frac{{{b^2}}}{{{a^2}}}} $,    ε>1

 

Если каноническое уравнение гиперболы вида

 

\[\frac{{{x^2}}}{{{a^2}}} — \frac{{{y^2}}}{{{b^2}}} =  — 1\]

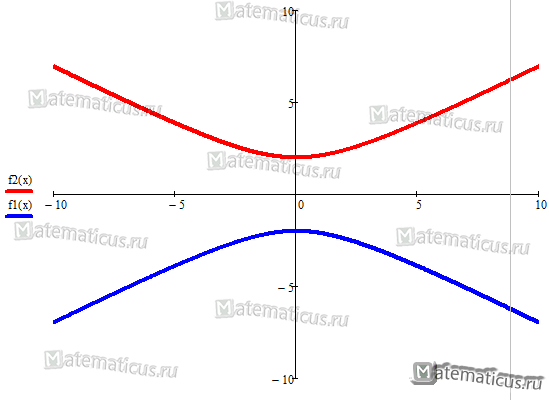
, то график гиперболы будет выглядеть примерно следующим образом

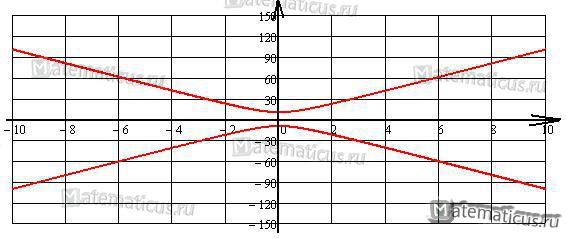
Построим гиперболу в mathcad