Парабола есть геометрическое место точек M, равноудалённых от данной точки F и данной прямой DD’:

FM=KM.

F  – фокус;

$F(\frac{p}{2};0)$

DD’ – директриса;

FC=p – расстояние от фокуса до директрисы называется параметром параболы;

CO=OF= $\frac{p}{2}$

O – точка, которая является вершиной параболы.

Каноническое уравнение параболы (ветви параболы направлены вправо)

y²=2px

если это уравнение принимает вид

y²=-2px

тогда ветви параболы направлены влево.

 

Уравнение директрисы DD’

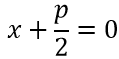
если поменять местами оси между собой, тогда

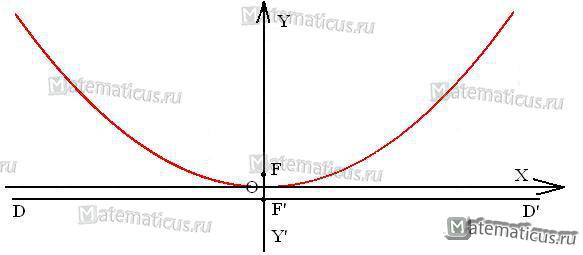
${x^2} = 2py,y + \frac{p}{2} = 0$

и график тогда будет выглядеть следующим образом (ветви направлены вверх)

 

 

Если в правой части уравнения отрицательный знак

x²= -2py

, то ветви параболы направлены вниз.

---

Уравнение вида

(y-y₀)²=-2p(x-x₀)

показывает смещение вершины параболы в точку (x₀;y₀)

Парабола относится к кривой второго порядка.

Пример задачи на определения параметров параболы.