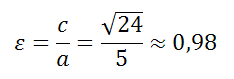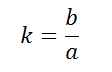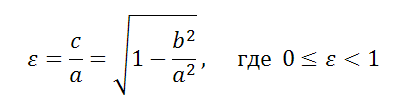Эллипс – геометрическое место точек M(x;y), сумма расстояний которых до двух данных точек F₁F₂ имеет одно и то же значение 2a:

F₁M+F₂M=2a 

точки F₁ и F₂ – называются фокусами эллипса;

расстояние F₁F₂ – фокусное расстояние и равно F₁F₂=2с;

a — большая полуось;

b — малая полуось;

c — фокальный радиус, то есть полу расстояние между фокусами;

p — фокальный параметр;

R_min – минимальное расстояние от фокуса до точки на эллипсе;

R_max — максимальное расстояние от фокуса до точки на эллипсе;

Каноническое уравнение эллипса

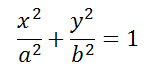
где

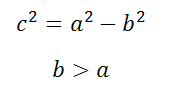
Фокальный параметр находится

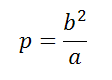Коэффициент сжатия эллипса (эллиптичность):

Сжатие эллипса

Коэффициент сжатия и эксцентриситет эллипса связаны соотношением

Эксцентриситет эллипса

Полуоси a, b и полуфокусное расстояние c эллипса выражаются через ε следующим образом

---

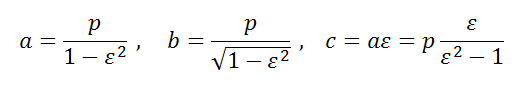
Пример 1

  Длина малой оси эллипса 134 м. Длина большой оси равна 140 м. Найти коэффициент сжатия k и сжатие α этого эллипса

Решение

---

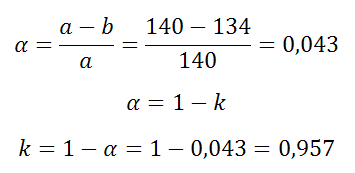
Пример 2

   Постройте кривую 4x²+9y²=36. Найдите фокусы, фокальный параметр и эксцентриситет.

Решение

 Делим обе части на 36 и получаем каноническое уравнение эллипса

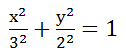
   a=3, b=2

Делаем чертёж

c²=a²-b²=3²-2²=9-4=5

Отсюда находим Фокусы F₁(-2,2;0) F₂(2,2;0)

Фокальный параметр находим следующим образом

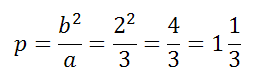
Эксцентриситет эллипса

---

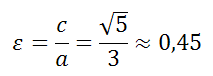
Пример 3
Постройте кривую 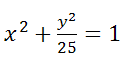. Найдите фокусы и эксцентриситет.

Решение
Уравнение запишем в виде

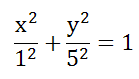
a=1, b=5
Это уравнение не является каноническим уравнением эллипса, так как b>a, а должно быть b<а. А если переобозначить оси, то есть x=x’ , y=y’, тогда уравнение примет вид:

И тогда a=5, b=1
Делаем чертёж

c²=a² − b²=5² −1²=25 − 1=24

Следовательно, фокусы в системе координат (x’;y’) имеют координаты (-4,9;0) и (4,9;0), а в системе (x;y) координаты

Эксцентриситет эллипса равен