Свойства математического ожидания случайной величины
Свойство 1. Математическое ожидание постоянной величины С=const равно ей самой:
М(С)=С
Свойство 2. Постоянный множитель можно выносить за знак математического ожидания:
М(СХ)=С⋅М(Х)
Свойство 3. Если X и Y — независимые случайные величины, то математическое ожидание суммы (разности) случайных событий равно сумме математических ожиданий этих событий:
М(Х±Y)=М(X)± М(Y)
Свойство 4. Если X и Y — независимые случайные величины, то математическое ожидание произведения случайных событий равно произведению математических ожиданий этих событий:
М(Х⋅Y)=М(X)⋅М(Y)
Свойство 5. Математическое ожидание отклонения СВ от её математического ожидания Х — M(X) равно нулю
М(Х-M(X))=0
Свойство 6. Математическое ожидание линейной функции от случайной величины представляется формулой
М(aХ+b)=aМ(Х)+b
Математическое ожидание M(X) определяется:
• для случайной дискретной величины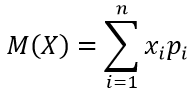
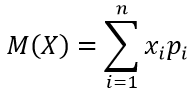
• для случайной непрерывной величины
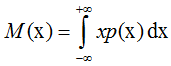
Пример
Найти математическое ожидание произведения двух независимых случайных величин X и Y. Законы распределения представлены в таблицах:
— для случайной величины X
| X | 2 | 4 | 8 |
| P | 0,25 | 0,45 | 0,3 |
— для случайной величины Y
| Y | 3 | 5 |
| P | 0,7 | 0,3 |
Решение
Найдем математическое ожидание случайной величины X:
M(X)=2·0.25+4·0,45+8·0.3=4.7
Найдем математическое ожидание случайной величины Y:
M(Y)=3·0.7+5·0,3=3.6
Так как случайные величины X и Y независимы, то в соответствии со свойством 4 имеем
M(XY)=M(X)·M(Y)=4.7·3.6=16.92
