Чтобы найти нормальное уравнение плоскости, заданной уравнением Ах+By+Cz+D=0, достаточно разделить обе части данного уравнения на:
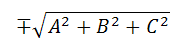
, причем верхний знак берется, когда D>0, и нижний, когда D<0; если же D=0, то можно взять любой знак.
Получаем уравнение:
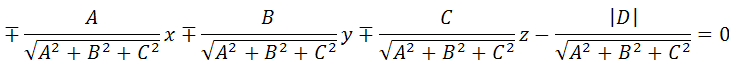
Пример 1
Привести к нормальному виду уравнение:
x-2у+2z-9=0
Решение
Делим обе части уравнения на:
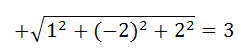
(перед радикалом —плюс, так как свободный член -9 отрицателен). Получаем:
Следовательно, р=3, cosα=1/3, cosβ=-2/3, cosγ=2/3
Пример 2
Привести к нормальному виду уравнение
x-2y+2z+9=0
Решение
Свободный член положителен и равен 9. Поэтому делим на
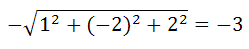
Получаем:
Следовательно,
р=3, cosα=-1/3, cosβ=2/3, cosγ=-2/3
р=3, cosα=-1/3, cosβ=2/3, cosγ=-2/3
Пример 3
Привести к нормальному виду уравнение
x-2y+2z =0
Решение
Так как D=0 (плоскость проходит через начало), то можно разделить либо на +3, либо на -3. В обоих случаях р=0. Величины в первом случае α, β, γ те же, что в примере 1, во втором — те же, что в примере 2.
