Свойства функции y=tgx

1. Область определения — x≠π/2+πn, n∈Z
2.  Область значения — E(f)=(-∞; +∞).
3. Периодическая T=π, непрерывная
4. Нечётная, tg(-x)=-tgx
5. На промежутке [-π/2+πn; π/2+πn] n∈Z функция возрастает.
6. Прямые x=π/2+πn, n∈Z — вертикальные асимптоты функции.
7. Корень x=πn, n∈Z
8. Экстремумов нет.

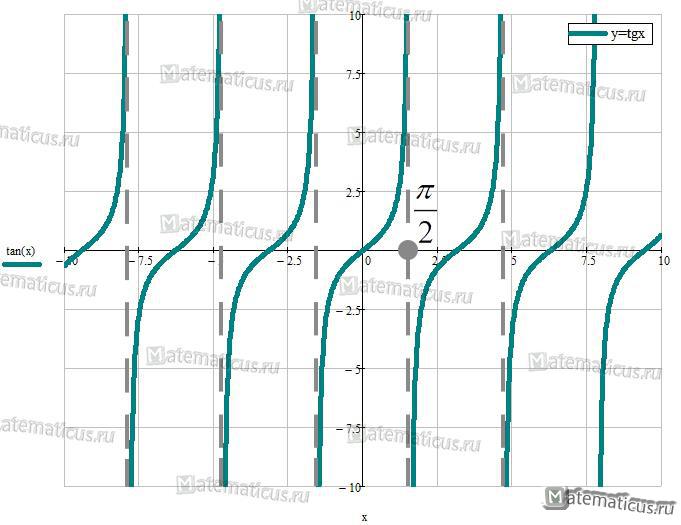
График функции y=tgx

---

Свойства функции y=сtgx

1. Область определения — x≠πn, n∈Z
2.  Область значения — E(f)=(-∞; +∞).
3. Периодическая T=π, непрерывная
4. Нечётная
5. На промежутке [πn; π+πn] n∈Z функция убывает.
6. Прямые x=πn, n∈Z — вертикальные асимптоты функции.
7. Корень x=π/2+πn, n∈Z
8. Экстремумов нет.

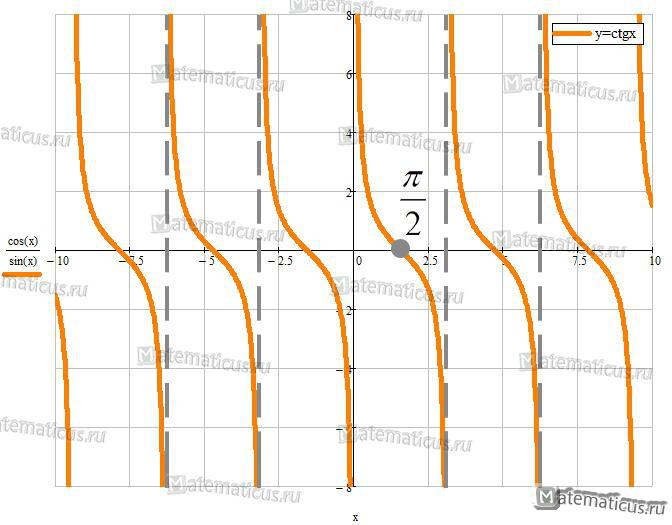 График функции y=ctgx

Подробное построение графиков функций y=tgx и y=ctgx см. здесь и здесь.