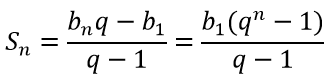Геометрическая прогрессия

Геометрическая прогрессия называется последовательность b₁, b₂, b₃ … b_n, у которой задан первый член не равный нулю b₁≠0, а каждый следующий, начиная со второго, равен предыдущему, умноженному на одно и то же число не равное нулю q≠0 и задаётся следующим равенством:

b_n+1 = b_nq

где q – знаменатель прогрессии и b₁≠0, q≠0.
Если q>0  и b₁>0, то геометрическая прогрессия возрастает, а если 0<q<1  и b₁>0 — то убывает.
Если q>0, то геометрическая прогрессия не монотонна.
Формула n-го члена геометрической прогрессии равна:

b_n = b₁⋅q^n-1

Формула знаменателя геометрической прогрессии:

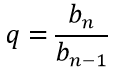
Формула суммы n первых членов геометрической прогрессии находится:

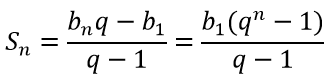
где q≠1 — знаменатель прогрессии, а S_n — сумма ее первых n членов,  S₁=b₁, S_n=b_n.
Если q = 1, получаем выражение

S_n=b₁⋅n

Сумма бесконечно убывающей геометрической прогрессии  |q|<1 определяется равенством:

при этом

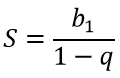
Характеристическое свойство:

b_n²=b_n-1⋅b_n+1

---

Пример 1
Найти q, если b₁=3, b₄=81
Решение
b₄ = b₁q³
81 = 3q³
q³=27
q=3

---

Пример 2
Дана геометрическая прогрессия 8; 4; 2; 1; 1/2; 1/4 …
Найти сумму этой прогрессии?
Решение
q = 4/8=1/2
$S = \frac{8}{{1 — \frac{1}{2}}} = 16$

---

Пример 3
Дана геометрическая прогрессия q=2; b₁=5
Найти сумму первых семи её членов?
Решение
${S_7} = \frac{{5\left( {{2^7} — 1} \right)}}{{2 — 1}} = 635$

---

Пример 4
Дана геометрическая прогрессия 16; 8; 4; 2; 1; 1/2; 1/4 …
Найти сумму b₁₀?
Решение
q = 8/16=1/2
b₁₀ = 16⋅(1/2)^9-1 = 1/16 = 0,0625

---

Калькулятор суммы геометрической прогрессии

Онлайн калькулятор суммы геометрической прогрессии

b₁=

q=

n=

---