Уравнение представлено в виде:
ax2 + bx +c =0
Тогда дискриминант находится по формуле:
D = b2 – 4ac
Замечание
Если D<0, то уравнение не имеет корней.
Если D=0, то уравнение имеет один корень.
Если D>0, то уравнение имеет два корня.
Формула для нахождения корней уравнения:
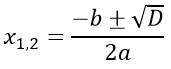
Разложение квадратного уравнения на множители:
ax2 + bx +c=a(x-x1)(x-x2)
Пример

Пример
Два автомобиля отправляются в 420-километровый пробег. Первый едет со скоростью на 10 км / ч большей, чем второй, и прибывает к финишу на 1 час раньше второго. Найти скорость автомобиля, пришедшего к финишу вторым
Решение
Пусть скорость второго автомобиля равна х км/ч, тогда скорость второго равна х+10 км/ч по условию задачи.
Пусть время второго автомобиля равно у ч, тогда:
ху=420
отсюда
$y=\frac{420}{x}$
Время первого автомобиля равно (у-1) ч.
Получаем уравнение:
(у-1)(х+10)=420
(420/х-1)(х+10)=420 /·х
(420-х)(х+10)=420х
420х+4200-x2-10x=420x
x2+10x-4200=0
D=(130)2
x1=(-10-130)/2 — отрицательный корень
х2=(-10+130)/2=120/2=60
Скорость автомобиля, пришедшего к финишу вторым равна 60 км/ч
