Решение квадратного уравнения по теореме Виета

1 способ

Квадратное уравнение вида

х² +рх + q = 0

удобно решать по теореме Виета

Если х₁ и х₂ таковы, что

х₁+х₂ =-р

х₁·х₂ = q

то х₁ и х₂ – корни квадратного уравнения

Пример
х²+х-30=0
Найдём такие корни уравнения, которые бы удовлетворяли условие
х₁+х₂ = -1
х₁·х₂ = -30
Такими корнями являются х₁=-6 и х₂=5.

---

2 способ
Теорема Виета
Имеется квадратное уравнение вида:

ах² +bх +с = 0

то по теореме Виета решение имеет вид

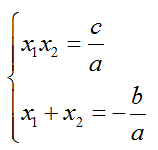
Пример
2х² + 5х – 3 = 0  
Найдём корни методом подбора
х₁ = – 3 и х₂ = 0,5
и эти корни удовлетворяет условию, т.е.
х₁·х₂= -3·0,5 = -1,5 = -3 : 2
х₁+х₂ = -3 + 0,5 = -2,5 = -5 : 2

---

Теорема Виета для кубического уравнения:

ax³+bx²+cx+d=0

Если x₁ x₂ и x₃ – корни уравнения, тогда

$x_1+x_2+x_3=\frac{{-b}}{{a}}$

$x_1·x_2+x_2·x_3+ x_1·x_3=\frac{{c}}{{a}}$

$x_1·x_2·x_3=\frac{{-d}}{{a}}$