Математическая постановка задачи о назначениях
Целевая функция имеет вид
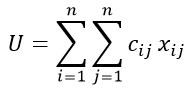
ограничения
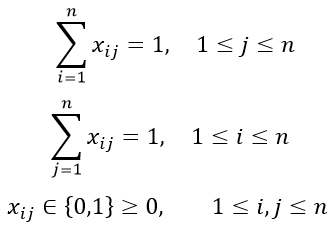
при этом матрица должна быть квадратной.
Рассмотрим на примере решение задачи максимизации целевой функции о назначениях венгерским методом
Допустим необходимо наилучшем образом распределить четыре автомобиля по четырем маршрутам. В матрице приведены оценки эффективности каждого автомобиля по каждому маршруту.
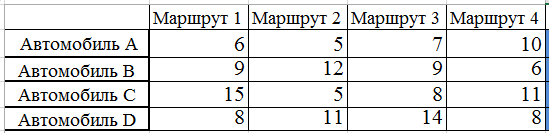
Решение
По строкам матрицы находим максимальное значение, так как по условию необходимо максимизировать целевую функцию (для задачи минимизации наоборот минимальное значение)
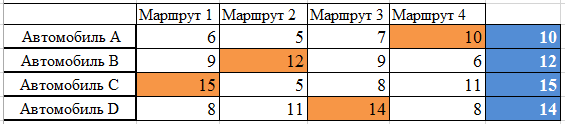
Затем последовательно из найденного максимального значения данной строки отнимаем каждое значение этой строки (поэлементно) при этом получаем нули в ячейках с максимальным значением и получаем матрицу вида
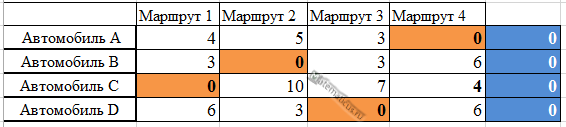
По столбцам матрицы находим минимальные значения
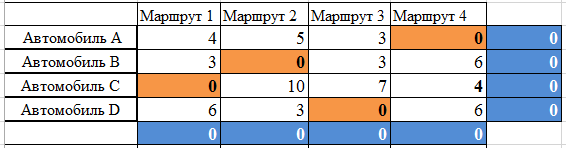
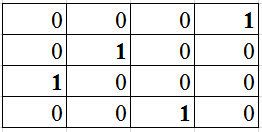
и если они все равны нулю и если выбранный ноль лежит только на пересечение единственного столбца и единственной строки, то оптимальное решение задачи венгерским методом о назначении найдено, то есть
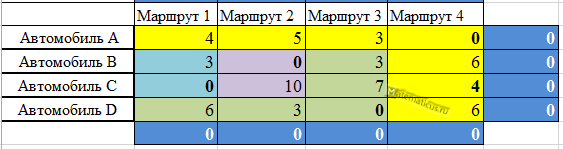
В нашем случае, наилучшее назначение:
Автомобиль A → Маршрут 4
Автомобиль B → Маршрут 2
Автомобиль C → Маршрут 1
Автомобиль D → Маршрут 3
Но на практике часто бывают ситуации, когда, например, какие-то из столбцов не равны нулю. Рассмотрим, опять же на примере. Пусть дана матрица вида и выполняем те же операции, что и ранее. 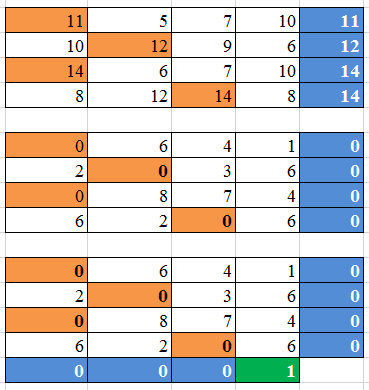
Также при решении задачи о назначении венгерским методом является необходимым выполнения следующего условия:
число исключений в таблице – минимальное.
в каждой строке и столбце таблицы должен стоять единственный выбранный ноль.
Исключаем столбцы и строки с нулями, получаем таблицу
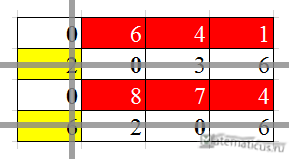
Затем из не исключенных значений таблицы (отмечено красным цветом), находим минимальное значение, в данном случае 1 и вычитаем его из ,опять же, не исключенных значений таблицы и прибавляем минимальное значение к тем значениям таблицы, которые находятся на перекрестке исключающих линий (отмечено желтым цветом).
Итак, оптимальное решение найдено, получаем матрицу вида
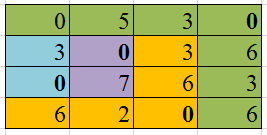
Таким образом, матрица назначений будем иметь вид: