Сумма n большого числа независимых равнозначных распределенных СВ X1,X2,X3…Xn имеет распределение, значение которого приближенно равно N[M(X);σ2(X)], где M(X)=na, σ2(X)=nσ2 (понятие центральной предельной теоремы Ляпунова)
Пример
В результате медицинского осмотра 900 призывников установлено, что их средняя масса на 1,2 кг больше средней массы призывников за один из предшествующих периодов. Какова вероятность этого отклонения, если среднее квадратичное отклонение массы призывников равно 0,8 кг?
Решение
Найдем дисперсию
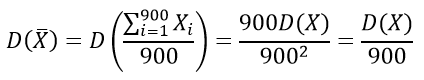
D(X)=σ2=0,82=0,64
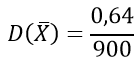
Вычислим СКО
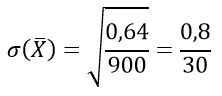
Имеем
![]()
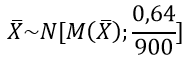
По формулам Лапласа находим решение 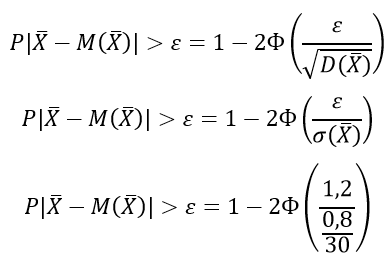
По таблице Лапласа находим значение
![]()
