Параллелограмм

Параллелограмм — это четырёхугольник, у которого противолежащие стороны параллельны AB//CD и BC//AD, то есть лежат на параллельных прямых.

Свойства параллелограмма:

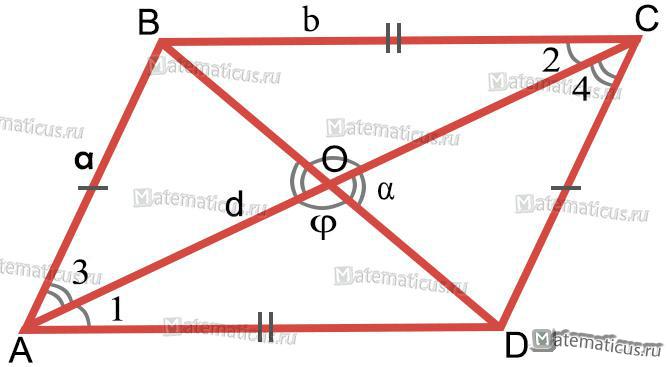
Рисунок 1 — Параллелограмм

1. У параллелограмма противолежащие стороны равны AD=BC и AB=CD

2. Противоположные углы равны

∠A=∠C, ∠B=∠D

∠AOB=∠DOC=∠α, ∠AOD=∠BOC=∠φ

3. Диагонали точкой пересечения O делятся пополам AO=OC, BO=OD

4. Сумма углов, прилежащих к одной стороне, равна 180°

5. Сумма квадратов диагоналей равна сумме квадратов всех сторон:

${\displaystyle d_{1}^{2}+d_{2}^{2}=2(a^{2}+b^{2})}$

Периметр параллелограмма определяется по формуле:

P=a+a+b+b=2a+2b=2⋅(a+b)

Формулы для определения площади параллелограмма:

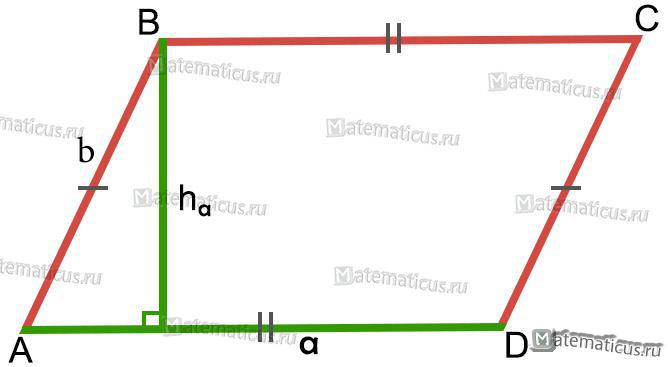
Рисунок 2 — Параллелограмм

Площадь параллелограмма S (см. рисунок 2) равна произведению стороны (основания AD) и опущенной на нее высоты (h_a):

S = a⋅h_a

a — основание, h_a — высота

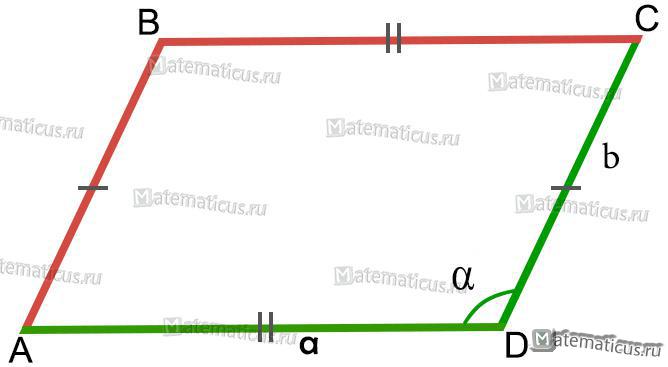
Рисунок 3 — Параллелограмм

Площадь параллелограмма S (см. рисунок 3) равна произведению прилежащих сторон AD и DC на синус угла между ними:

S = a⋅b⋅sinα

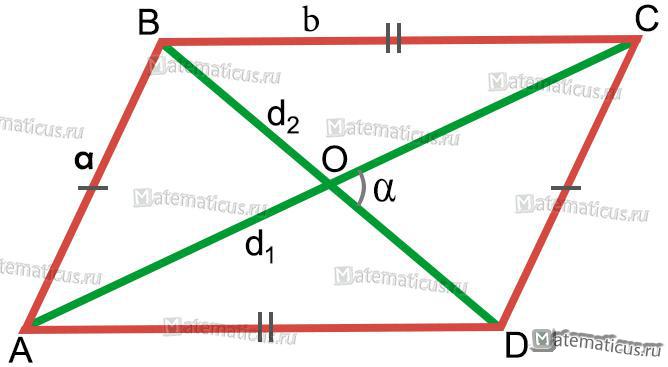
Рисунок 4 — Параллелограмм

Площадь параллелограмма S (см. рисунок 4) равна половине произведения диагоналей AC и BD на синус угла между ними:

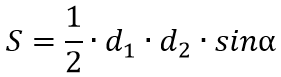
 Длина диагонали параллелограмма находится по теореме Пифагора:

 $d = \sqrt {{a^2} + {b^2}} $