The Monte Carlo method refers to a numerical stochastic approximate mathematical method using a random number sensor. For the first time, the Monte Carlo method was used to calculate the number π in the Buffon problem.
For example, the General formula for determining an arbitrary area of the shape S will look like:
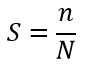
n — the number of points that fall within the area of the calculated shape;
N is the total number of points, N>100.
The accuracy of the method depends on the number of repetitions of the experience, that is, the greater the number of experiences (repetitions), the higher the accuracy of the method.
Consider the Monte Carlo method for calculating the area of a circle inside a square, and the probability of falling points on the coordinate plane obeys the uniform distribution law of a random variable.
For clarity, the solution of the problem based on the Monte Carlo method is presented in graphical form.
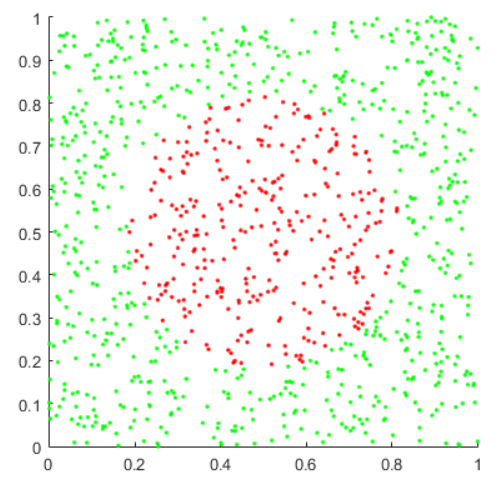
Modeling using the Monte Carlo method at 1000 points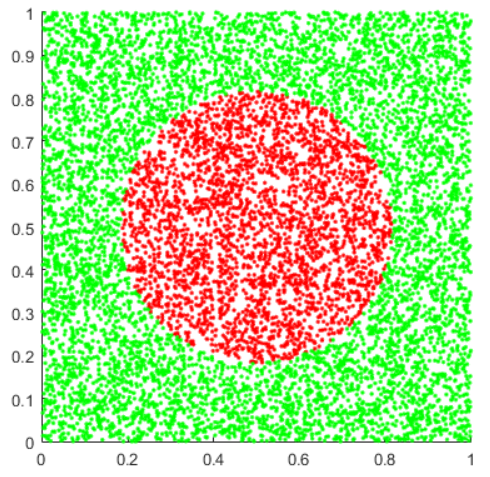
Modeling using the Monte Carlo method at 10000 points
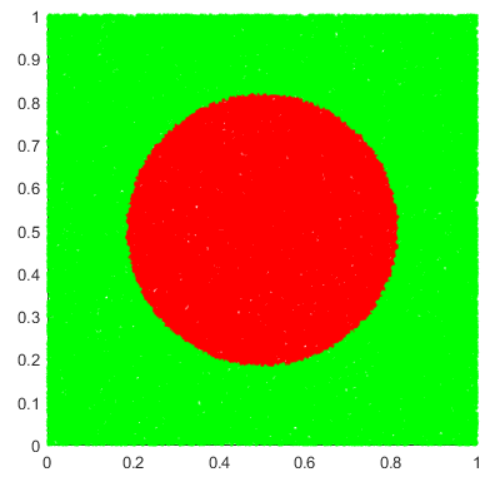
Modeling using the Monte Carlo method at 100000 points
The method is used for studying random processes, calculating the area of figures (numerical integration of functions), simulating annealing, mathematics, physics, Economics, etc.
