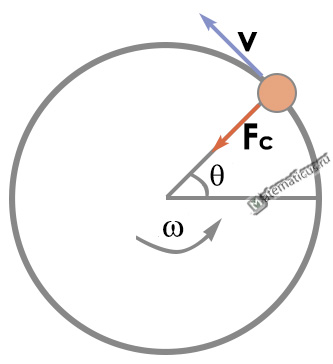
Movement along a circle always occurs with acceleration and is curved, since the distance is not equal to the displacement and the trajectory occurs along a circle. The speed when moving around a circle is directed tangentially, and the acceleration to the center of the circle. When a body moves uniformly around a circle, the speed does not change modulo, but changes in the direction, v=const, a⊥v.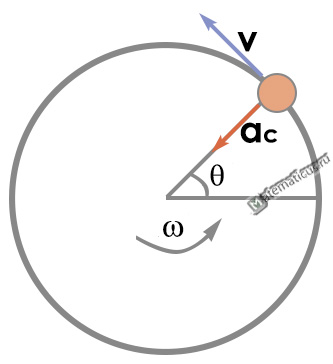
The period or time of a single period is determined by the formula:
$T = \frac{t}{N}$
T – period, s;
t – time, s;
N – number of revolutions.
Formula for determining the frequency (i.e. the number of revolutions per second):
$f = \frac{1}{T}$
$T = \frac{1}{f}$
f — frequency, Hz (Hertz) or s-1.
The linear speed is found by the formula:
$V = \frac{{2\pi R}}{T}$
V — speed, m/s.
R is the radius of the circle, m.
The formula for the angular (cyclic) speed (that is, the number of revolutions per 2π):
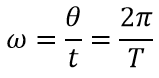
ω — angular velocity, rad/s
φ — the angle at which the body turns, radian (rad)
Centripetal acceleration:
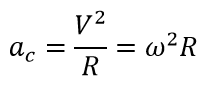
ac — centripetal acceleration, m/s2
The centripetal force is determined by the formula:
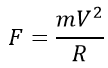
The centripetal force is directed to the center of the circle, figure below