Buffon’s problem of throwing a needle
Method Buffon is based on the Monte Carlo method and consists of throwing a needle on a plane drawn at a distance from each other with parallel lines. This method is also used for calculating the number π. The greater the number of repetitions of the experience, the more accurate the result will be.
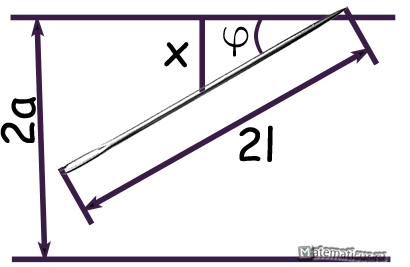
The plane is divided by parallel lines that are separated from each other at a distance of 2a. On the plane at random throw a needle of length 2l (2l≤2a), φ — angle. Find the probability that the needle will cross a straight line.
Solution
Graphically, the Buffon problem can be represented as follows:
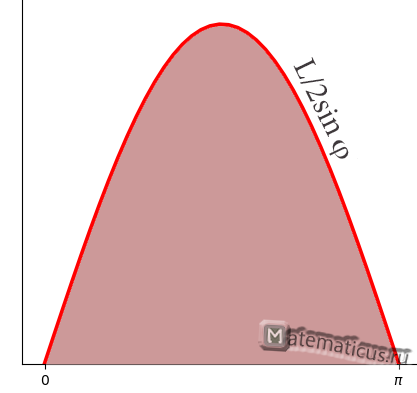
Calculated the probability by calculating the integral:
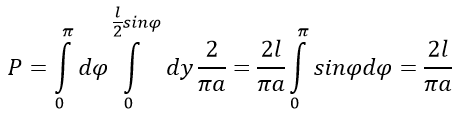
Experimentally, using the Monte Carlo method, the probability is determined by the formula:
P≈[number of casts]/[number of intersections]
The number π can be approximated by the Monte Carlo method using the formula:
π≈2L*[number of casts]/a*[number of intersections]
a — distance between lines.
If we assume that the length of the needle is equal to the distance between the lines, the expression is defined by the formula:
π≈2*[number of casts]/[number of intersections]
In practical probability calculations, we also use the condition that parallel lines are located at a distance of two needle lengths from each other.
