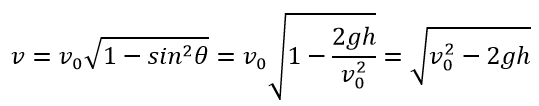Movement of a body thrown at an angle to the horizon

The movement of a body thrown at an angle to the horizon moves along a parabola. The maximum flight range of a body thrown at an angle to the horizon is achieved at a throwing angle of 45⁰. The founder of this task of dynamics is Galileo Galilei.

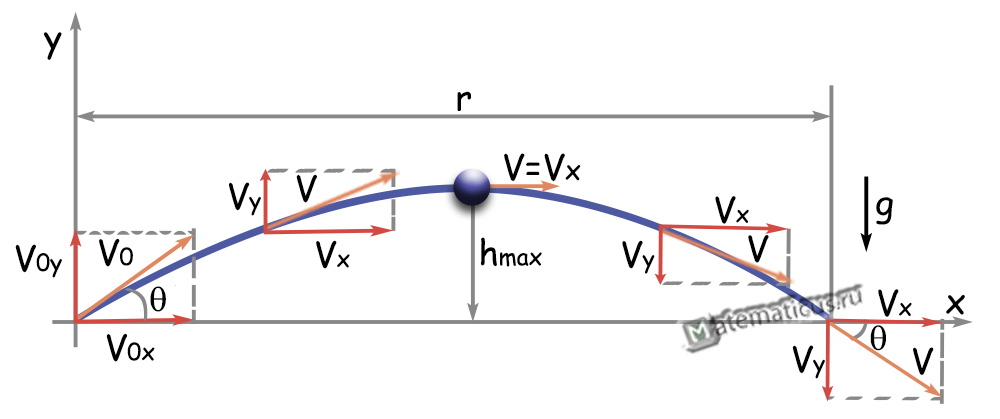
$x\left( t \right) = t{v_0}cos\theta; $

$y\left( t \right) = t{v_0}sin\theta — \frac{{g{t^2}}}{2}$

$y = xtg\theta — {x^2}\frac{g}{{v_0^2co{s^2}\theta }}$

X-аxis:

V_x=V_0x

V_0x=V₀cosθ

Y-аxis:

V_y=V_0y−gt

V_0y=V₀sinθ

The speed of the object at any point is determined by:

$v = \sqrt {v_x^2 + v_y^2} $

The formula for determining the flight of time from the equation 0=V₀sinθ−gt:

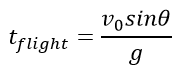
Formula for determining the maximum flight altitude from the equation:

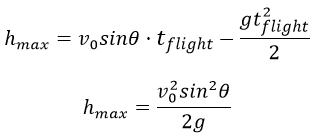
The total movements time is calculated using the formula:

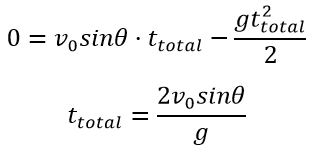
The drop time is calculated using the formula:

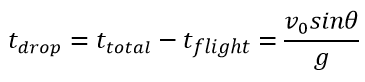
Throw range formula:

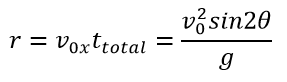
Speed at the highest point of the trajectory: