Формула Тейлора имеет вид:
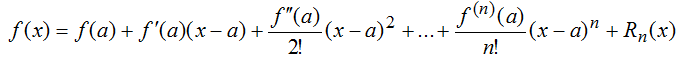
При а=0 имеем ряд Маклорена, тогда формула для разложения функций в ряд Маклорена примет вид:
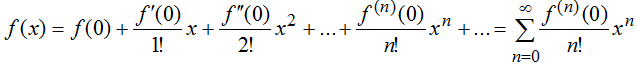
Разложения некоторых элементарных (в том числе тригонометрических — cosx, sinx, arctgx, arcsinx, shx, chx, ex, логарифмических) функций в ряд Маклорена:
14598