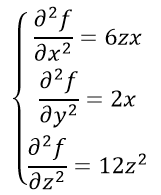Частные производные функции нескольких переменных

Формула производной частной функции F′(x₁,x₂,x₃…x_n) первого порядка имеет вид:

Аналогично формула производной функции нескольких переменных второго порядка имеет вид:

Рассмотрим нахождение частных производных функции нескольких переменных, в данном примере производную по x и по y.

Замечание

При вычислении частной производной по одной переменной, остальные все принимаются за константу.

---

Пример

Найти частные производные  $\frac{{\partial z}}{{\partial x}};\,\,\frac{{\partial z}}{{\partial y}}$ функции

$z = \sin \left( {4x} \right) + {x^2}{y^3}$

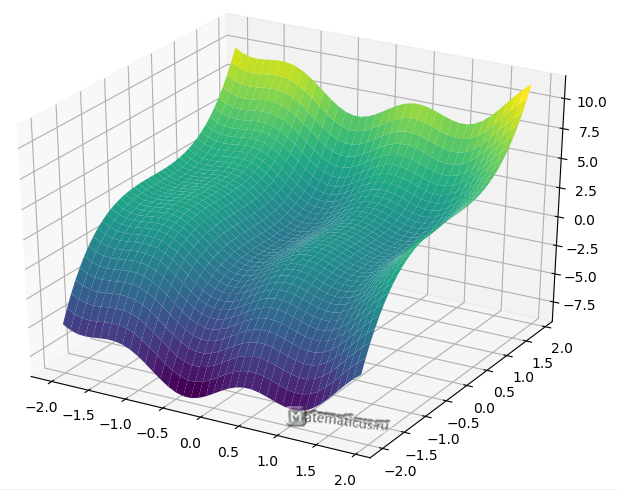График функции нескольких переменных $z = \sin \left( {4x} \right) + {x^2}{y^3}$

Решение

---

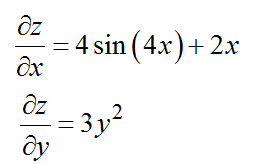
Пример
Найти частные производные функции трех переменных функции первого и второго порядка

f(x,y,z)=x³z+y²x+z⁴–3

Решение
По формуле найдем частные производные функции трех переменных первого порядка

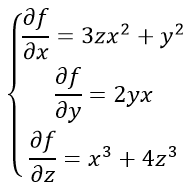
Отсюда получаем частные производные второго порядка