Теорема Кронекера-Капелли
Для того чтобы система линейных алгебраических уравнений (СЛАУ) с n неизвестными
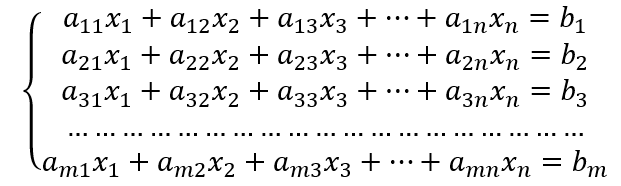
была совместной, необходимо чтобы ранг основной матрицы был равен рангу расширенной матрицы, то есть
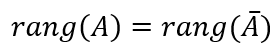
Замечание
Если ранг совместной СЛАУ меньше числа неизвестных, то данная СЛАУ имеет бесконечно множество решений, а если ранг совместной СЛАУ равен числу неизвестных, то СЛАУ имеет только одно решение.
Пример
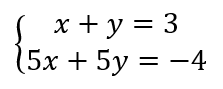
Совместима ли данная система линейных алгебраических уравнений?
Решение
Так как
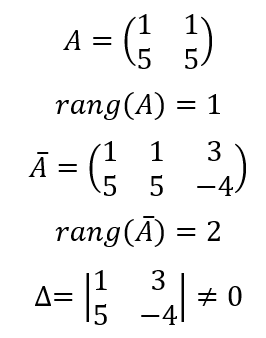
то данная система уравнений несовместна.
![]()
