Линии кривых в полярной системе координат

Семейство роз Гранди

Уравнение имеет вид:

ρ=asinkφ

a — радиус лепестка;

k — положительный параметр, отвечает за количество лепестков.

Свойство:

|sin(kφ)| ≤1

Рисунок 1 — роза с тремя лепестками ρ=sin3φ

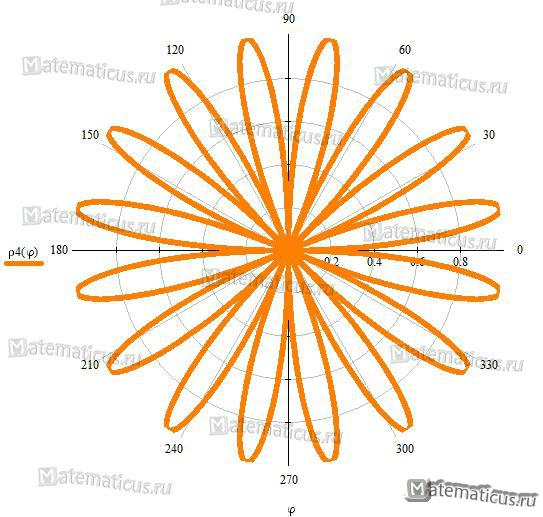
Рисунок 2 — роза с 16 лепестками ρ=sin8φ

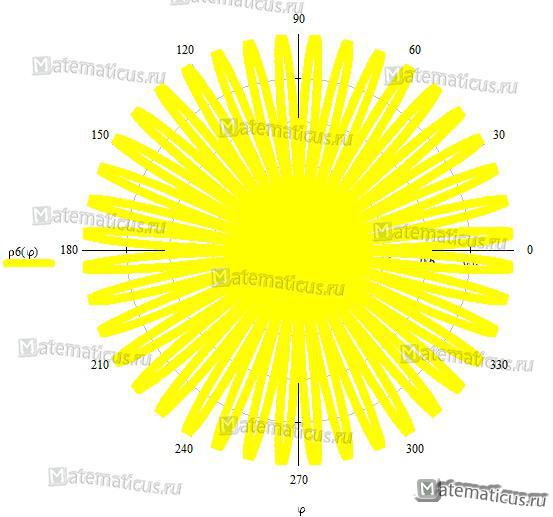
Рисунок 3 — семейство роз Гранди — напоминает ромашку ρ=sin20φ

 

Рисунок 4 — семейство роз Гранди — линия похожа на зрачок глаза ρ=sin100φ

---

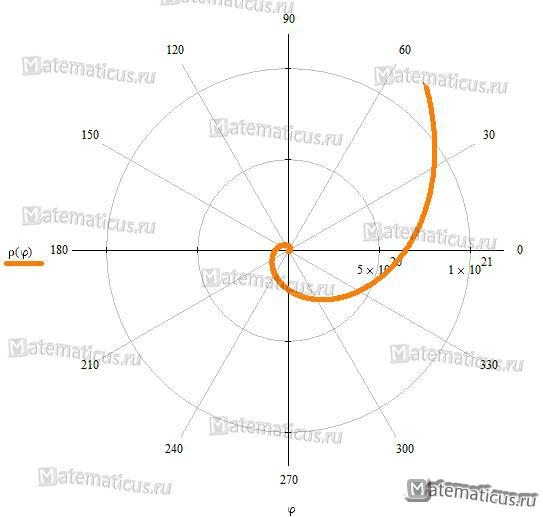
Логарифмическая спираль

Уравнение логарифмическая спираль (трансцендентная кривая) в полярных координатах:

ρ = 2^aφ

---

Кардиоида

Кардиоида частный случай улитки Паскаля.

Уравнение кардиоиды (перев. греч. сердце и вид) в полярных координатах:

ρ=a(1+Cοsφ)

---

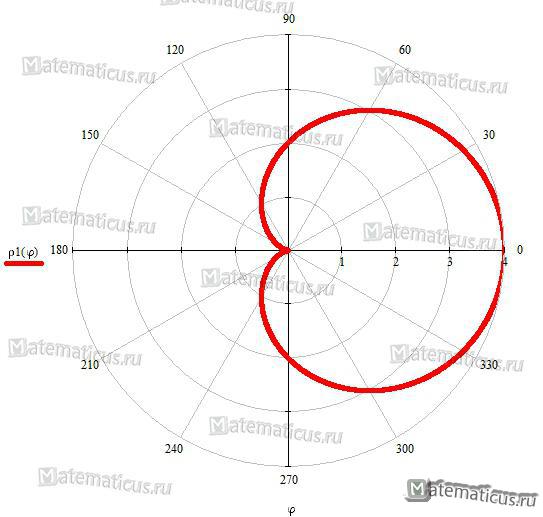
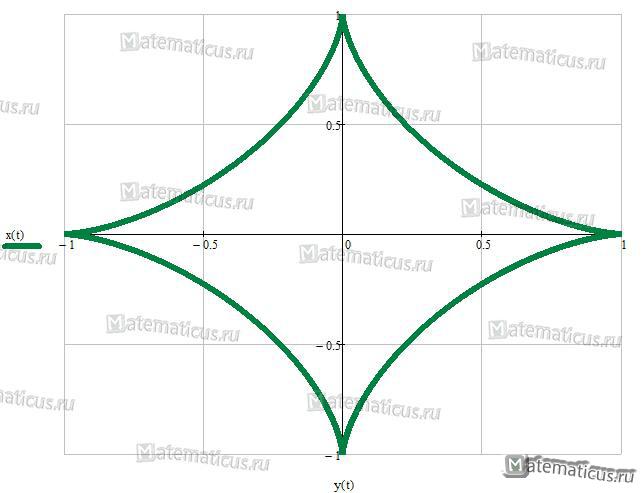
Астроида

Уравнение астроиды (перев. греч. звезда и вид):

x^2/3 + y^2/3 = a^2/3

или

x = a cos³t

y = a sin³t

---

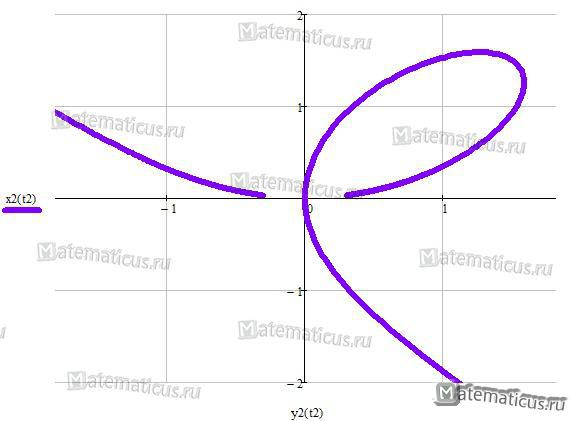
Строфоида

Уравнение строфоиды (перев. греч. крученая лента, поворот):

y² (a — x)= x² (a + x)

Уравнение строфоиды в полярной системе координат:

$\rho  =  — \frac{{a\cos 2\varphi }}{{\cos \varphi }}$

---

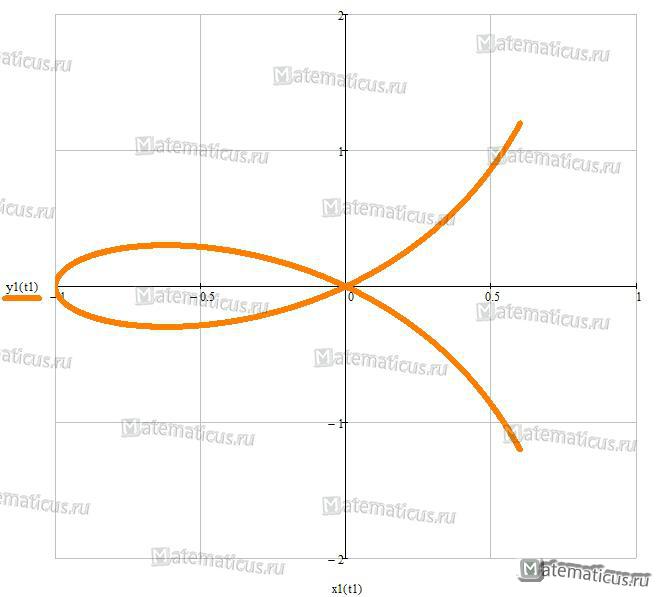
Декартов лист

Уравнение декартова листа:

x² + y² — 3axy = 0

Уравнение декартова листа в полярной системе координат:

$$\rho = \frac{{2a\cos \phi \sin \phi }}{{{{\cos }^2}\phi + {{\sin }^2}\phi }}$$

---

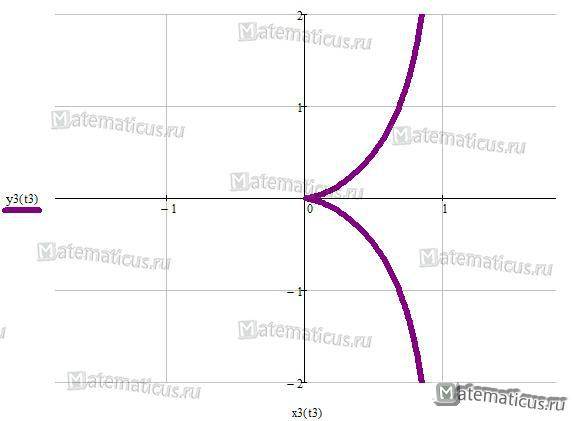
Циссоида

Уравнение циссоиды Диоклеса (перев. греч. плющ, вид) в прямоугольной системе координат:

y² = x³/(a + x) 

Параметрическое уравнение циссоиды:

x =  at²/(1 + t²) 

x =  at³/(1 + t²) 

Уравнение циссоиды в полярной системе координат:

$$\rho  = \frac{{2a{{\sin }^2}\varphi }}{{\cos \varphi }}$$

---

Циклоида

Параметрическое уравнение циклоиды:

x = R (t — sint)

y = R (1 — cost)

---

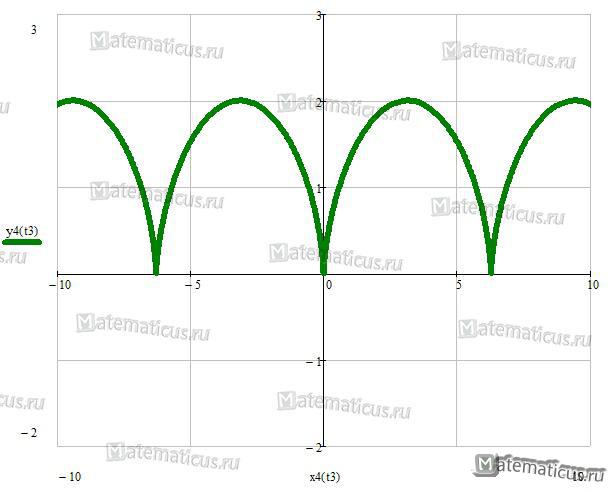
Кохлеоида

Уравнение кохлеоиды (трансцендентная кривая) в полярных координатах:

$\rho  = \frac{{\pi a}}{2}\frac{{\sin \varphi }}{\varphi }$

 

---

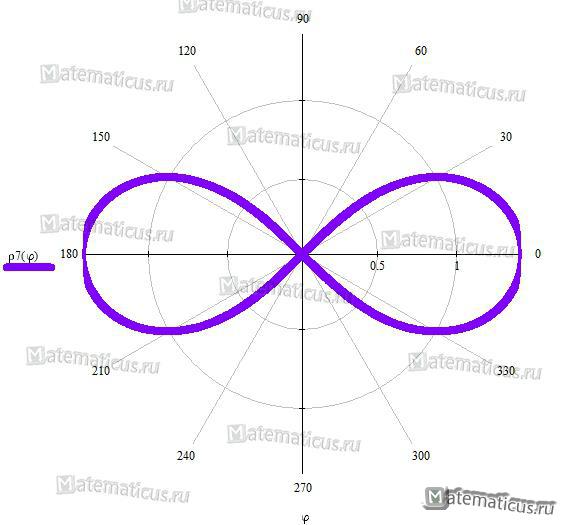
Лемниската Бернулли

Уравнение лемниската Бернулли в прямоугольных координатах:

(x² + y²)² = a² (x² — y²)

Уравнение лемниската Бернулли в полярных координатах:

р² = a²соs2φ

---

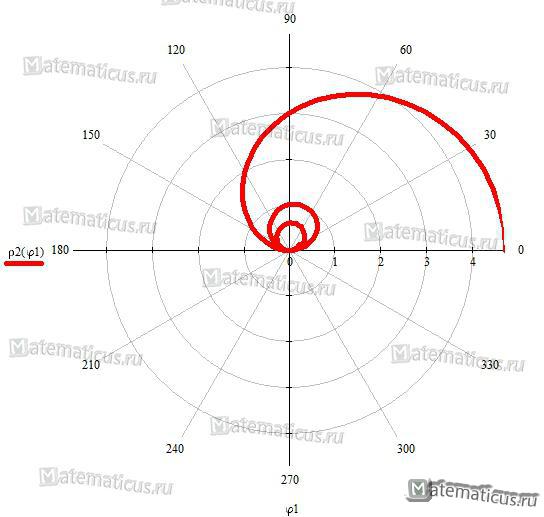
Архимедова спираль рассмотрена здесь подробно.

---

Применяя математические уравнения замечательных кривых, можно получить вот такие геометрические линии.

 

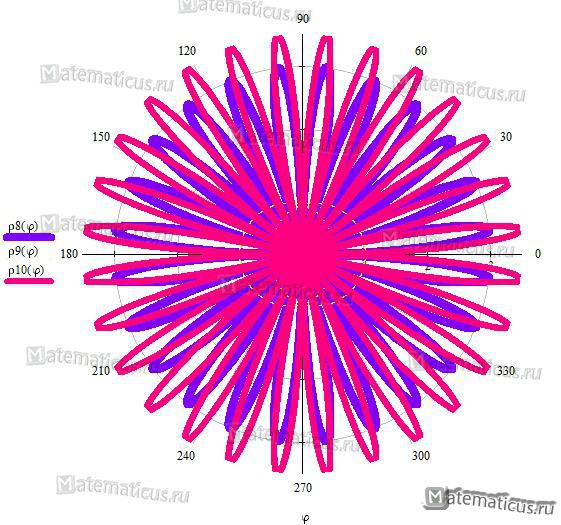
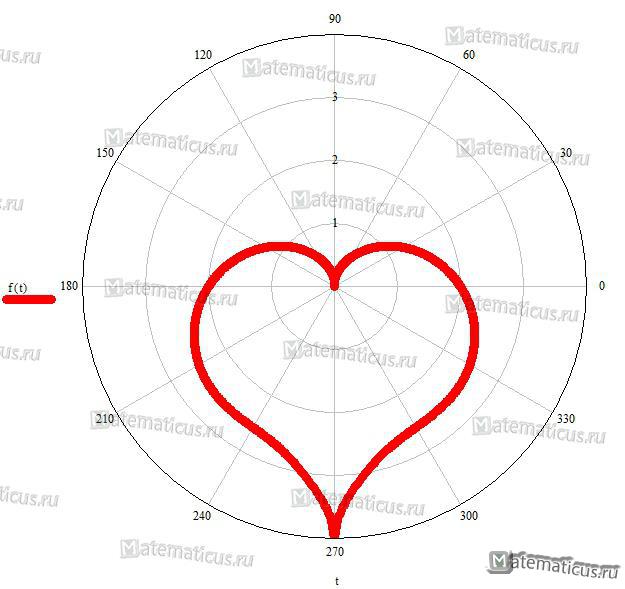
Математическое уравнение сердца имеет вид:

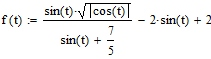
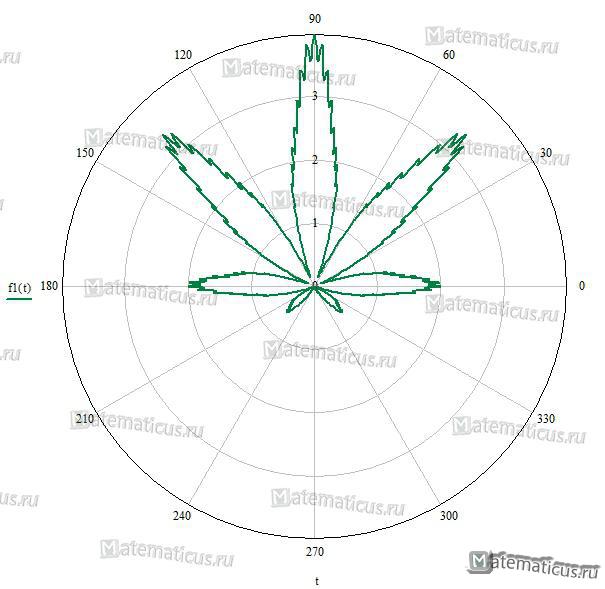
Лист клена, уравнение: