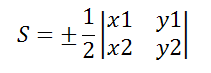Площадь треугольника на плоскости

Пусть точки A(x₁;y₁), B(x₂;y₂), C(x₃;y₃) – вершины треугольника, тогда площадь треугольника выражается формулой

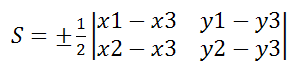
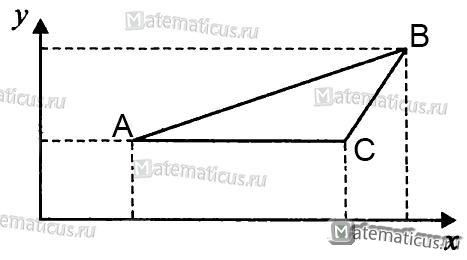
В формуле правая сторона — это определитель второго порядка.

Площадь треугольника является положительной величиной и поэтому перед определителем берём знак «плюс», в случае, если значение положительно, и минус в противном случае, то есть отрицательно.

Примечание
Если вершина C треугольника совпадает с началом координат, то есть x₃=y₃=0, то формула площади треугольника примет вид

и вычисляется как определитель второго порядка

---

Пример
Найти площадь треугольника с вершинами A(2;-4), B(-5;-6) и C(1;3)

Решение
Пусть примем  A за первую вершину, B — за вторую и C — за третью, тогда находим:

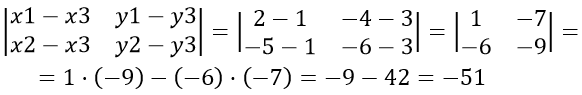
,так как получился отрицательный знак, следовательно перед определителем берём знак «минус»

\[S = ( — \frac{1}{2})\cdot( — 51) = 25,5\]

Если вершины треугольника переобозначим немного в другом порядке, допустим, первой вершиной A, второй вершиной  C и третьей вершиной B, тогда получим выражение:

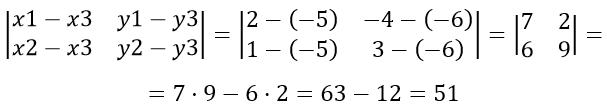
В этом случае, необходимо взять знак «плюс« и получим снова площадь треугольника S=25,5