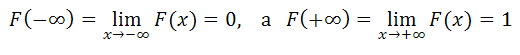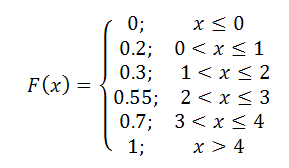Функцией распределения случайной величины X называется функция F(x), задающая вероятность того, что случайная величина X принимает значение меньшее x, то есть
F(x) = р(Х<х)
Также функцию F(x) называют интегральной функцией распределения.
Плотность распределения вероятности (также называют дифференциальной функцией) функции распределения определяет непрерывную случайную величину.
Случайная величина X называется непрерывной, если её функция распределения непрерывна на всей числовой оси.
Обозначение: F(x)
Свойства функции распределения случайной величины
1. Функция распределения есть неотрицательная функция, заключенная между нулем и единицей:
0≤F(x)≤1
2. Функция монотонно возрастающая, т. е. если xj > xi , то F(xj) > F(xi)
3.
4. P(a≤X<b) = F(b) — F(a)
Пример 1 (Функция распределения дискретной случайной величины)
По заданному закону распределения случайной величины X, вычислить функцию распределения дискретной случайной величины.
| X | 0 | 1 | 2 | 3 | 4 |
| P | 0,2 | 0,1 | 0,25 | 0,15 | 0,3 |
Решение
Если x≤0, то F(x)=Р(Х<0)=0, следовательно событие при Р(Х<0) невозможно.
Если 0<x≤1, то F(x)=Р(Х<1)=Р(Х=0)=0.2
Если 1<x≤2, то F(x)=Р(Х<2)=Р(Х=0)+Р(Х=1)=0.2+0.1=0.3
Если 2<x≤3, то F(x)=Р(Х<3)=Р(Х=0)+Р(Х=1)+Р(Х=2)=0.2+0.1+0.25=0.55
Если 3<x≤4, то F(x)=Р(Х<4)=Р(Х=0)+Р(Х=1)+Р(Х=2)+Р(Х=3)=
=0.2+0.1+0.25+0.15=0.7
Если x>4, то F(x)=Р(Х<4)=Р(Х=0)+Р(Х=1)+Р(Х=2)+Р(Х=)+Р(Х=4)=
=0.2+0.1+0.25+0.15+0.3=1
Получаем функцию распределения дискретной СВ в аналитическом виде:
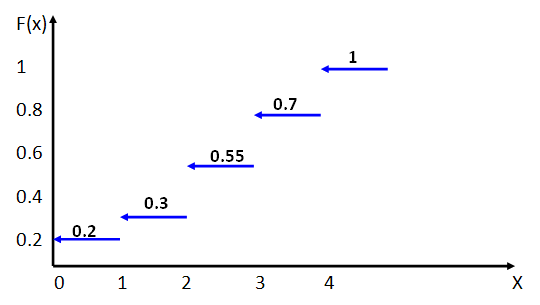
График функции распределения дискретной случайной величины имеет вид:
Пример 2 (Функция распределения непрерывной случайной величины)
Пример для непрерывной случайной величины X можно посмотреть здесь.
Показана функция распределения для показательного (экспоненциального) закона распределения
7909