Формула бинома Ньютона имеет вид:
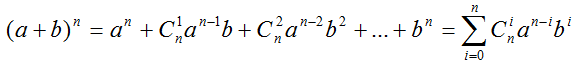
![]()
$C_n^k$ — число сочетаний из n элементов по k.
(a+b)n — разложение степени бинома;
Биномиальный коэффициент в соответствии с формулой сочетание без повторений определяется по формуле:
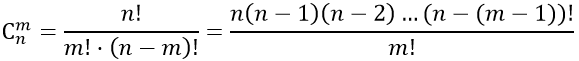
где m=0,1,2,3…n
Биномиальные коэффициенты можно получить с помощью треугольника Паскаля (операция сложения).
Формула разложения бинома n-ой степени:
![]()
Бином Ньютона необходим, чтобы уменьшить (упростить) вычисления.
Пример
(a+b)0=1
(a+b)1=a+b
(a+b)2=a2+2ab+b2
(a+b)3=a3+3a2b+3ab2+b3
(a+b)4=a4+4a3b+6a2b2+4ab3+b4
Бином Ньютона связан с треугольником Паскаля



Треугольник Паскаля все знают. Доказать разложение бинома Ньютона методом математической индукции — простая задача. А как вывести формулу для коэффициентов (не показать и объяснить, а вывести!) вы не знаете. Поэтому и повторяете как попугай всё что и на остальных сайтах. Так математику не выучить!
Формула коэффициентов выводится с использованием закономерности сочетание без повторений. Если вы пришлете нам материал в данном направлении мы будем вам благодарны. Спасибо за отзыв)